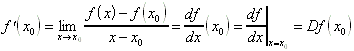
6. Differentialrechnung
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
Die Tangente einer Funktion f an der Stelle x ist eine Gerade, die die Funktion f an der Stelle x berührt bzw. unter dem Winkel a = 0 schneidet.
6.0.2 Limes des Differenzenquotienten, Ableitung der Funktion f an der Stelle x:
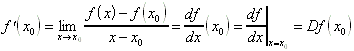
Die Differenzierbarkeit kann eingeschränkt sein (s. Stetigkeit). Man unterscheidet deshalb linksseitige und rechtsseitige Differenzierbarkeit.
Ist die Ableitung an der Stelle x positiv, so ist die Funktion dort monoton steigend, ist die Ableitung negativ, so ist sie dort monoton fallend. Ist sie null, so liegt ein
Extrempunkt oder Terrassenpunkt vor.
6.2 Ableitungen von reellwertigen Funktionen mehrerer Veränderlicher und von vektorwertigen Funktionen
6.2.1 Vektorwertige Funktionen und deren Ableitung:
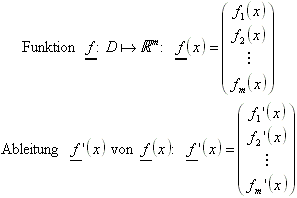
f'(x) ist der Richtungsvektor der Tangente an die Kurve f im Punkt (x, f(x)).
6.2.2 Partielle Ableitung einer reellwertigen Funktion f:
Die partielle Ableitung einer Funktion f(x) nach xj in x0 lautet:
Dabei werden außer xj alle Veränderlichen als Konstanten angenommen und entsprechend behandelt.
6.2.3 Totale Ableitung bei einer Funktion f(x,y,z) im ![]() :
:
Geometrisch stellt die totale Ableitung f'(x) in ![]() die Tangentialebene an f(x) in x0 dar.
die Tangentialebene an f(x) in x0 dar.
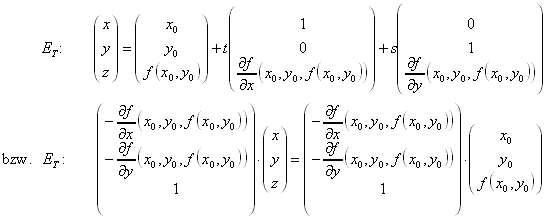
Als Gradient der Funktion f in x0 wird dieser (transponierte)Vektor a bezeichnet:
Hierbei ist ![]() der Nabla-Operator, der in Kapitel 16.3 näher beschrieben wird.
der Nabla-Operator, der in Kapitel 16.3 näher beschrieben wird.
Als Gradient oder Gradientenfeld von f bezeichnet man:
6.2.5 Partielle Ableitung einer vektorwertigen Funktion:
Die partiellen Ableitungen einer solchen Funktion werden nur komponentenweise erklärt. Es gilt:
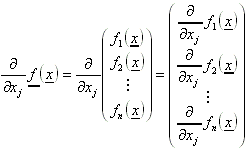
Die totale Ableitung an einer Stelle x0 ergibt eine Matrix. Für sie gilt:
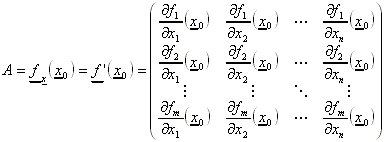
Dies ist eine (m,n)-Matrix.
Wird ein weiteres Mal abgeleitet, so entsteht die sogenannte Hessesche Matrix.
Beispiel zu vektorwertigen Funktionen:
Gegeben als Funktion ist das Vektorprodukt. Gesucht ist die erste Ableitung.
6.2.6 Ableitungsregeln für vektorwertige Funktionen:
Analog zu reellwertigen Funktionen einer Veränderlichen gelten der Faktorsatz und die Summenregel.
Die Produktregel für m = 1:
Es handelt sich also um eine (n,1)-Matrix.
Für weiteres zum Nabla-Operator ![]() siehe Kapitel 16.3 .
siehe Kapitel 16.3 .
Die Kettenregel ![]()
Kapitel 7: Potenzreihen