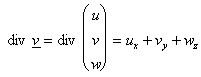
16. Integralsätze und Vektoranalysis
             Kein Frame mit dem Inhaltsverzeichnis ?  => Frameset laden

16.1 Satz von Gauß in Ebene und Raum

16.1.1 Divergenz eines Vektorfeldes:

Es gilt (übertragbar in Ebene und Raum):

16.1.2 Satz von Gauß in der Ebene:

Sei G ein geeignetes Gebiet des (sternförmig). Sei weiter die Randkurve so parametrisiert, daß G "links" von liegt. Es sei v ein stetig differenzierbares Vektorfeld. Dann gilt:

16.1.3 Satz von Gauß im Raum:

Sei G ein geeignetes Gebiet des (sternförmig). Die Randfläche sei durch x(u,v) so parametrisiert, daß nach "außen" zeigt. Es sei v ein stetig differenzierbares Vektorfeld. Dann gilt:

16.1.4 Fluß von v durch :

Als Fluß von v durch wird das Integral bezeichnet.

16.1.5 Zirkulation von Vektorfeldern:

Sie ist für alle geschlossenen C definiert als

.

Ist Z = 0 bzw. ,

dann heißt das Vektorfeld v zirkulationsfrei.

16.2 Satz von Stokes

16.2.1 Rotation eines Vektorfeldes:

Die Rotation rot v ist definiert als:

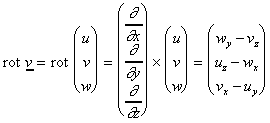
Ist rot v = 0, so handelt es sich um ein wirbelfreies Feld. v ist dann ein Potentialfeld im entsprechenden Gebiet.

16.2.2 Satz von Stokes:

Es sei F ein Flächenstück definiert auf einem Parameterbereich . Dieser sei so beschaffen, daß der Satz von Gauß anwendbar ist.

Außerdem sei die Abbildung , die F bestimmt, zweimal stetig differenzierbar. Ist nun das Vektorfeld v auf einem Gebiet, das F enthält, stetig differenzierbar, so gilt der

Satz von Stokes:

16.2.3 Vektorpotential:

Es sei stetig differenzierbar und G sternförmig. Es existiert ein "Vektorpotential" a als ein in stetig differenzierbares Feld mit , wenn in folgendes gilt:

16.3 -Rechnung (Nablarechnung)

16.3.1 -Operator:

Er wird folgendermaßen definiert:

16.3.2 Rechenregeln:

Für skalare Felder j, y und für Vektorfelder f, g gilt:

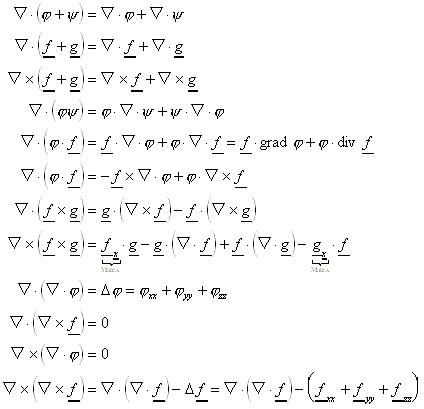
16.4 Der Green'sche Integralsatz

16.4.1 Green'scher Integralsatz:

Es sei ein Gebiet im , so daß der Satz von Gauß gilt. Sind u, v auf zweimal stetig differenzierbar, dann gilt mit dem nach außen gerichteten Normaleneinheitsvektor n von G:

Hierbei ist D der Laplace-Operator.

16.4.2 Anwendung:

Es sei G ein Gebiet, so daß der Satz von Gauß gilt, und es sei U zweimal stetig differenzierbar in . Gilt Du = 0 auf G, so ist für x₀ aus G:

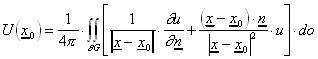
16.5 Exakte Differentialgleichungen

16.5.1 Exakte Differentialgleichungnen:

Eine Differentialgleichung der Form

mit stetigen Funktionen heißt in G exakt, wenn es eine stetig differenzierbare Funktion F gibt die die folgende Bedingung erfüllt:

F muß also das Potential des Vektorfeldes sein.

Häufig schreibt man exakte Differentialgleichung in der Form
.

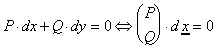Für das Potential F gilt:

16.5.2 Exakte Differentialgleichungen in sternförmigen Gebieten:

In sternförmigen Gebieten mit stetigen Funktionen gilt Folgendes:

ist genau dann exakt, wenn

gilt. Diese Bedingung heißt Integrabilitätsbedingung.

16.5.3 Spezielle Vektorpotentiale:

Hat das Potential F die Form

,

dann ist f(x) Lösung der Differentialgleichung .

16.5.4 Singuläre Punkte von exakten Differentialgleichungen:

Diese ergeben sich aus diesem Gleichungssystem:

16.5.5 Integrierender Faktor m(x,y):

Als integrierenden Faktor bezeichnet man den zweimal stetig differenzierbaren Term m(x,y), der nicht null ist, welcher sich aus dieser Bedingung ergibt.

Damit werden nicht exakte Differentialgleichungen zu exakten Differentialgleichungen.

Die Lösung erhält man dann wieder aus
.

16.5.6 Bestimmung von integrierenden Faktoren für bestimmte Differentialgleichungen:

16.5.6.1 Stellt eine nur von x abhängige Funktion dar, dann ist:

16.5.6.2 Stellt eine nur von y abhängige Funktion dar, dann ist:

16.5.7 Implizite Lösungen von nicht exakten Differentialgleichungen:

16.5.7.1 Wesentlich verschieden heißen zwei integrierende Faktoren m und n, wenn es keine reelle

Zahl l gibt, so daß

16.5.7.2 Implizite Lösung:

Anhang: Tabellen und Kurzreferenzen