eine Parameterdarstellung der Kurve C. Es sei 
eine stetige Funktion. Dann heißt 15. Kurven- und Oberflächenintegrale
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
15.1 Orientierte und nicht orientierte Kurvenintegrale
15.1.1 Orientiertes Kurvenintegral:
Sei eine Parameterdarstellung der Kurve C. Es sei eine stetige Funktion. Dann heißt
orientiertes Kurvenintegral von f längs C.
Andere Schreibweise:
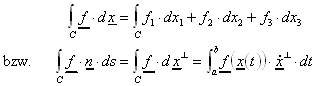
15.1.2 Nicht orientiertes Kurvenintergal:
Ist 
stetig, so heißt
nicht orientiertes Kurvenintegral von j längs C.
15.1.3 Eigenschaften von Kurvenintegralen, Rechenregeln:
15.1.3.1 Bei zulässigen Parametertransformationen verändern orientierte und nicht orientierte Kurvenintegrale ihren Wert nicht.
15.1.3.2 Für reelle a, b , stetige Skalarfelder j, y , und stetige Vektorfelder f, g gilt:
15.1.3.3 Weitere Eigenschaften sind:
15.1.3.4 Es gelten folgende Abschätzungen:
15.1.4 Potential eines Vektorfeldes:
Ist C eine geschlossene Kurve innerhalb eines sternförmigen Gebietes, und existiert ein skalares Feld j, so daß
ist, dann gilt immer
j heißt Potential des Vektorfeldes f.
Unter einem sternförmigen Gebiet versteht man ein Gebiet im  , in dem
es mindestens einen Punkt gibt, von dem aus es Geraden zu jedem
anderen Punkt in dem Gebiet geben kann, die die Grenzlinien des Gebietes
nicht überschneiden. Von diesem Punkt ausgehende Strahlen
durchschneiden die Grenzlinien des Gebietes demnach genau einmal. |  |
15.2 Orientierte und nicht orientierte Oberflächenintegrale
Allgemein betrachtet man Oberflächenintegrale ebenso wie Kurvenintegrale.
15.2.1 Orientiertes Oberflächenintegral:
Sei 
eine Parameterdarstellung des Flächenstückes F. Es sei 
ein stetiges Vektorfeld. Dann heißt
orientiertes Oberflächenintegral von f auf F.
Ähnlich setzt man das komponentenweise zu integrierende Integral
.
15.2.2 Nicht orientiertes Oberflächenintegral:
Ist 
eine stetige skalare Funktion so heißt
nicht orientiertes Oberflächenintegral von j auf F.
15.2.3.1 Oberflächenintegrale verändern ihren Wert nicht, falls eine zulässige Parametertransformation durchgeführt wird.
15.2.3.2 Für reelle a, b , stetige Funktionen j, y , und stetige Vektorfelder f, g gilt:
15.2.3.3 Weitere Eigenschaften sind:
15.2.3.4 Es gelten folgende Abschätzungen:
15.2.4 Explizit gegebene Funktionen:
Ist F explizit gegeben durch eine Funktion z = f(x,y), dann läßt sich sagen:
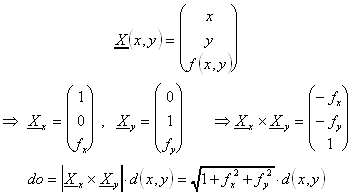
Kapitel 16: Intergalsätze und Vektoranalysis
