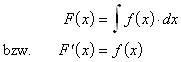
9. Integralrechnung
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
9.1 Definition der Stammfunktion
9.1.1 Für die Stammfunktion F(x) einer Funktion f(x) gilt Folgendes:
Wenn eine solche Funktion F(x) existiert, so heißt f(x) integrierbar und
das (bestimmte) Riemann - Integral von f in den Grenzen x1 = a (untere Grenze) und x2 = b (obere Grenze).
9.1.2 Hauptsatz der Differential- und Integralrechnung:
Eine im Intervall [a,b] stetige Funktion f(x) mit der Stammfunktion F(x) schließt mit der x-Achse die Fläche
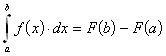
ein.
9.2 Eigenschaften und Anwendungen von Integralen
9.2.1 Bogenlänge einer Raumkurve K im Intervall [a,b]:
Für sie gilt allgemein:
![]()
Der letzte Term gilt auch für Kurven im ![]() .
.
9.2.2 Wichtige Eigenschaften von Riemann-Integralen:
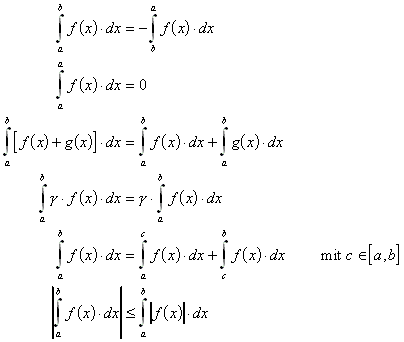
Prinzip: Im Allgemeinen eine Umformung und Rückfühung von Integralen auf Grundintegrale.
Beispiel:
![]()
9.3.2 Die Ableitung der Funktion tritt im Integranden auf:
1. Beispiel:
![]()
2. Beispiel:
![]()
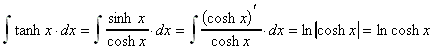
9.3.3 Die Substitutionsmethode:
Allgemein gilt:
1. Beispiel:
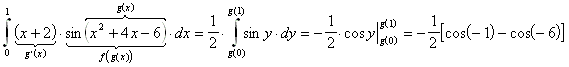
2. Beispiel:
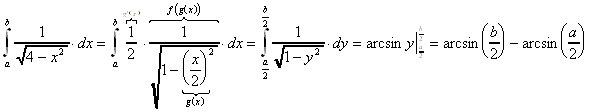
Allgemein gilt:
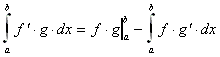
1. Beispiel:
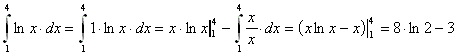
2. Beispiel:
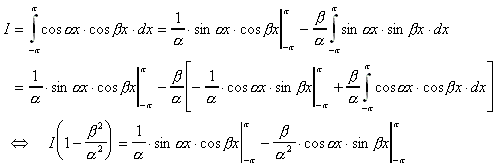
Für ![]() gilt:
gilt:
Hieraus folgt dann: I = 0.
9.3.5 Integration rationaler Funktionen (Partialbruchzerlegung):
9.3.5.1 Integrale der Form 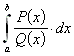 mit Grad (P) > Grad(Q) werden mit Hilfe von Polynomdivision vereinfacht und - wenn kein Rest bleibt - sofort integriert.
Andernfalls benötigt man die Methode der Partialbruchzerlegung.
mit Grad (P) > Grad(Q) werden mit Hilfe von Polynomdivision vereinfacht und - wenn kein Rest bleibt - sofort integriert.
Andernfalls benötigt man die Methode der Partialbruchzerlegung.
9.3.5.2 Bei der Betrachtung von Integralen der Form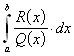 mit Grad (R) < Grad(Q) kommt der Fundamentalsatz der Algebra zur Anwendung. Dabei wird
Q(x) in Faktoren reeller Nullstellen und ggf. Polynome der nicht-reellen Nullstellen zerlegt.
mit Grad (R) < Grad(Q) kommt der Fundamentalsatz der Algebra zur Anwendung. Dabei wird
Q(x) in Faktoren reeller Nullstellen und ggf. Polynome der nicht-reellen Nullstellen zerlegt.
![]()
Nicht-reelle Nullstellen treten als ![]() auf.
auf.
Im weiteren Lösungsverlauf werden auch die Vielfachheiten kn der reellen Nullstellen xn und die Vielfachheiten lt der nicht-reellen Nullstellen zt berücksichtigt.
Die Partialbruchzerlegung von ![]() ist dann eindeutig bestimmt durch:
ist dann eindeutig bestimmt durch:
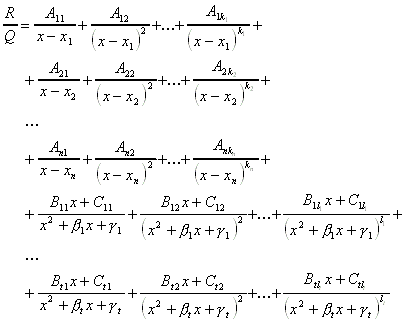
Es gibt dann die Möglichkeit, für die Lösung einen Koeffizientenvergleich mit der ursprünglichen Funktion durchzuführen, indem man beide Seiten der
obenstehenden Gleichung mit Q(x) multipliziert und das dann aus der Gleichheit der Koeffizienten erhaltene lineare Gleichungssystem nach den unbekannten
Koeffizienten auflöst und integriert.
Eine andere Möglichkeit ist das "Zuhalte-Verfahren" (Zitat eines Assistenten) zur Bestimmung eines Koeffizienten Apq: In Gedanken wird die Gleichung auf
beiden Seiten mit Nenner des Bruchs bei Apq erweitert und die Nullstelle xp des ursprünglichen Integranden eingesetzt. Für die Bestimmung der anderen
Koeffizienten wird dieses Verfahren wiederholt, unter Umständen muß man die dann vorliegende Gleichung mit Polynomdivision vereinfachen, bevor man fortfährt.
Beispiel: Gesucht ist das unbestimmte Integral der folgenden Funktion:
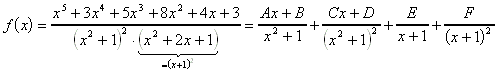
Zuhalte-Verfahren zur Bestimmung von F: Mit ![]() multiplizieren und dann x = -1 einsetzen:
multiplizieren und dann x = -1 einsetzen:
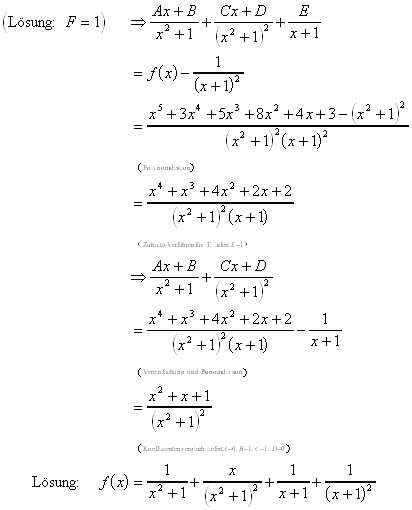
Für das Integral ergibt sich dann Folgendes:
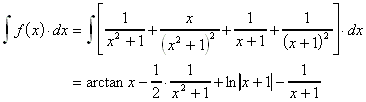
9.3.6 Integration rationaler Funktionen von sin und cos:
Zunächst wird substituiert:
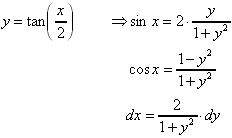
Danach wird integriert, ggf. muß noch eine Partialbruchzerlegung durchgeführt werden.
9.3.7 Integration rationaler Funktionen von sinh und cosh:
Substitution:
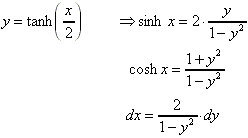
9.3.8 Integration von Potenzreihen:
Es gilt:
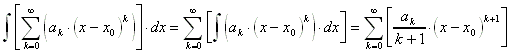
Für das Volumen V eines um die x-Achse rotationssymmetrischen Körpers mit f(x) als Funktion der Berandung gilt im Intervall [a,b]:
![]()
9.4 Integrale bei Funktionen mehrerer Veränderlicher
9.4.1 Zweidimensionale Integrale:
Das Volumen V zwischen der Funktion f(x,y) und der x-y-Ebene im Bereich ![]() beträgt:
beträgt:
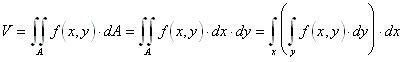
Beispiel: Gesucht ist das Volumen des Tetraeders, dessen Ecken in (0,0,0), (a,0,0), (0,b,0) und (0,0,c) sind. Die Gleichung der entsprechenden Ebene liefert den gesuchten Inhalt:
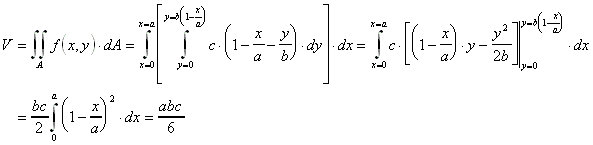
9.4.2 Dreidimensionale Integrale:
Analog zu zweidimensionalen Integralen gilt:
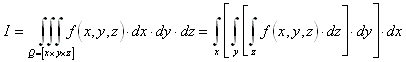
Beispiel: Gesucht ist das Volumen V einer (zentrosymmetrischen) Kugel mit Radius R.
Es gilt gemäß der obenstehenden Gleichung:
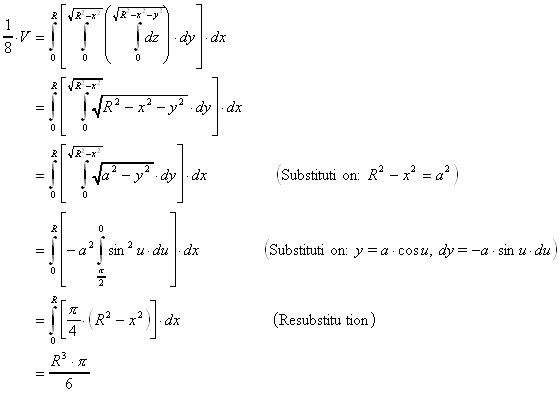
Das Kugelvolumen beträgt dann
.
9.4.3 Masse m und Schwerpunkt eines Körpers:
Für sie gilt:
9.5.1 Konvergentes uneigentliches Integral:
1. Bedingung: Für alle reellen a,b aus dem Definitionsbereich (a,b) [z.B. ![]() ] der
] der
gegebenen Funktion f ist f integrierbar.
2. Bedingung: Es gibt ein c aus (a,b), so daß folgende Integrale existieren:

Uneigentliches Integral:
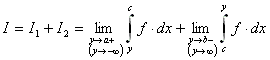
9.5.2 Vergleichskriterium für uneigentliche Integrale:
9.5.2.1 Konvergiert 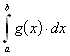 und ist
und ist ![]() , so konvergiert auch
, so konvergiert auch 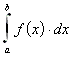 .
.
9.5.2.2 Divergiert 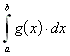 , während
, während ![]() ist, so divergiert auch
ist, so divergiert auch 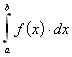 .
.
Ist die Funktion ![]() monoton fallend und gilt ständig
monoton fallend und gilt ständig ![]() , so kann man sagen:
, so kann man sagen:
Es konvergiert 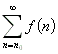 , wenn
, wenn 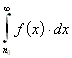 konvergiert.
konvergiert.
9.6 Parameterabhängige Integrale
9.6.1 Stetigkeit von Parameterintegralen:
Das folgende Parameterintegral ist im Definitionsbereich von f(x,t) stetig:
Ist im Parameterintegral auch ft(x,t) stetig, dann gilt für die Ableitung F'(t):
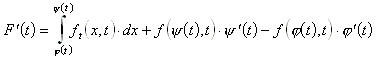
9.7 Integration durch Reihenentwicklung, spezielle nichtelementare Funktionen
9.7.1 Die Gammafunktion ![]() oder das Eulersches Integral zweiter Gattung:
oder das Eulersches Integral zweiter Gattung:
Als Gammafunktion wird folgendes uneigentliche Integral definiert:
Die Gammafunktion hat folgende Eigenschaften:
Letztere Eigenschaft erlaubt die Erweiterung des Begriffs der Fakultät auf beliebige reelle Zahlen:
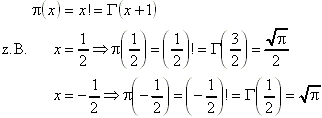
Sie wird definiert als:
![]()
Für |x| < ![]() gilt:
gilt:
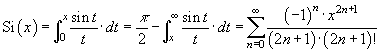
Für 0 < x < ![]() gilt:
gilt:
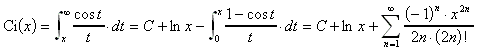
9.7.5 Integralexponentialfunktion:
Für -![]() < x < 0 und 0 < x <
< x < 0 und 0 < x < ![]() gilt:
gilt:
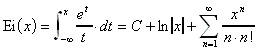
Ist 0 < x < ![]() , so spricht man vom Cauchyschen Hauptwert.
, so spricht man vom Cauchyschen Hauptwert.
Für 0 < x < 1 und 1 < x < ![]() gilt:
gilt:
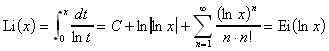
Ist 1 < x < ![]() , so spricht man vom Cauchyschen Hauptwert.
, so spricht man vom Cauchyschen Hauptwert.
9.7.7 Gausssches Fehlerintegral:
Für |x| < ![]() gilt:
gilt:
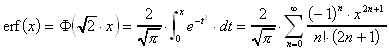
Eigenschaften:
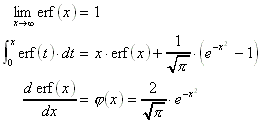
9.8 Literaturhinweise zu Integralen
9.8.1 Bronstein / Semendjajew / Musiol / Mühlig:
Taschenbuch der Mathematik (1. Auflage, 1993): Seiten 265ff
| Logarithmische Integration | Seite 267 |
| Substitutionsmethode | Seite 268 / Seite 273 / Seite 275 |
| Partialbruchzerlegung | Seite 269 |
| Integration irrationaler Funktionen | Substitutionstabelle Seite 273f |
Integral enthält den Term bzw. die Terme | Bronstein / Semendjajew / Musiol / Mühlig: |
ax + b | Seite 741 |
| Seite 743 |
| Seite 745 |
| Seite 747 |
| Seite 748 |
allgemeine Beispiele zu Partialbruchzerlegung | Seite 748 |
| Seite 749 |
| Seite 750 |
| Seite 752 |
| Seite 754 |
| Seite 756 |
| Seite 758 |
Sinusfunktion | Seite 761 |
Cosinusfunktion | Seite 763 |
Sinus- und Cosinusfunktion | Seite 766 |
Tangensfunktion / Cotangensfunktion | Seite 770 |
Hyperbelfunktionen | Seite 771 |
Exponentialfunktion | Seite 772 |
Logarithmische Funktionen | Seite 774 |
Inverse trigonometrische Funktionen | Seite 775 |
Inverse Hyperbelfunktionen | Seite 777 |
Kapitel 10: Tensoren, Quadratische Formen