10. Tensoren, Quadratische Formen
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
10.0.1 Linearitätseigenschaft einer Abbildung:
Gegeben seien Vn als ein n-dimensionaler Raum sowie die Abbildung ![]() .
.
A heißt lineare Abbildung, wenn folgende Eigenschaften erfüllt sind:
10.0.2 Eigenwerte und Eigenvektoren: Allgemeine Definition siehe Kapitel 3.3
Beispiel: Gesucht werden die Eigenwerte und Eigenvektoren der Matrix A:
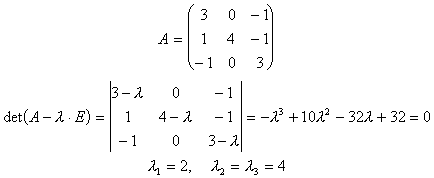
Die Eigenvektoren werden dann nach bekanntem Prinzip berechnet:
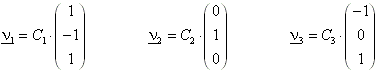
Es sei bemerkt, daß die Eigenvektoren einer Matrix eine Orthogonalbasis darstellen, falls die Matrix symmetrisch ist. Es gilt dann:
2. Beispiel: Eigenvektoren als Orthogonalbasis zur folgenden Matrix A
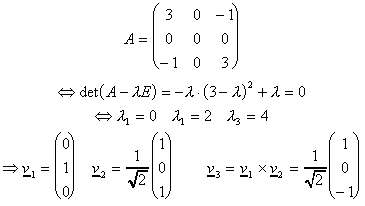
Bei der Aufstellung einer solchen Basis ist allerdings darauf zu achten, daß l1< l2 < l3 ist.
10.1 Tensoren, Koordinatendarstellungen
Als erste Etappe zur Definition allgemeiner Tensoren werden an dieser Stelle Tensoren als geometrische Objekte eingeführt. Gilt beispielsweise für die Verzerrung f der vier Punkte P, Q, R, S eines Parallelogramms die Vorschrift
so spricht man bei f von einem geometrischen Tensor 2. Stufe.
Ist eine allgemeine Abbildung A aus Vn linear, so spricht man von einem Tensor 2. Stufe.
Vektor ![]() fest:
fest:
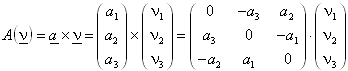
Der Vektor ![]() sei fest. Dann ist die Projektionsabbildung ein Tensor:
sei fest. Dann ist die Projektionsabbildung ein Tensor:
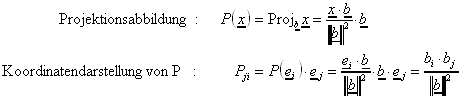
10.1.5 Dyadisches Produkt zweier Vektoren:
Die Vektoren ![]() seien fest. Dann ist folgende Abbildung D ein Tensor:
seien fest. Dann ist folgende Abbildung D ein Tensor:
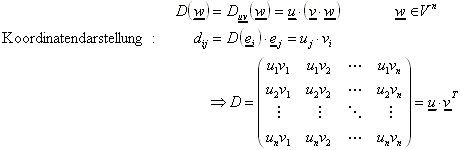
Es sei der Vektor ![]() mit ||u||=1. Dann stellt
mit ||u||=1. Dann stellt ![]() (siehe oben) eine Spiegelung an der Ebene
(siehe oben) eine Spiegelung an der Ebene ![]() dar. Su heißt Spiegelungstensor.
dar. Su heißt Spiegelungstensor.
Die Koordinatendarstellung dieser Spiegelung lautet:
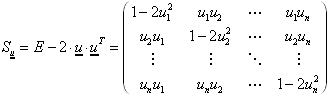
Es folgt daraus:
1. Su ist eine symmetrische Matrix.
2. Su ist orthogonal.
3. Su ist zu sich selbst invers: ![]()
10.1.7 Drehtensor (Drehung im Raum ![]() um eine feste Drehachse):
um eine feste Drehachse):
Es sei der Vektor ![]() , (Voraussetzung: ||a||=1).
, (Voraussetzung: ||a||=1).
Die Drehung Da(j) aller Vektoren um den Winkel j gegen den Uhrzeigersinn um eine Drehachse der Richtung a ist ein Tensor. Es gilt:
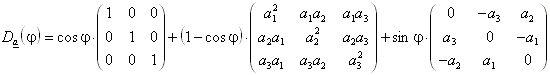
Die Determinante det(D) eines Drehtensors beträgt immer +1.
10.1.8 Eulersche Drehmatrizen:
Die drei Spezialfälle der allgemeinen Dretensoren ergeben sich durch Eisetzen der drei Basisvektoren e1, e2 und e3 für a. Es enstehen dabei Drehtensoren um die drei Achsen des Koordinatensystems.
Drehung um die e3-Achse (z-Achse):
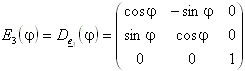
Drehung um die e2-Achse (y-Achse):
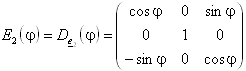
Drehung um die e1-Achse (x-Achse):
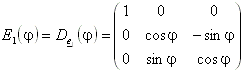
10.1.9 Verkettung der Eulerschen Drehmatrizen:
Ist D eine Drehmatrix, dann gibt es drei Winkel a, b, g, so daß Folgendes gilt:
![]()
Allgemein ausgedrückt lautet diese Drehmatrix so:
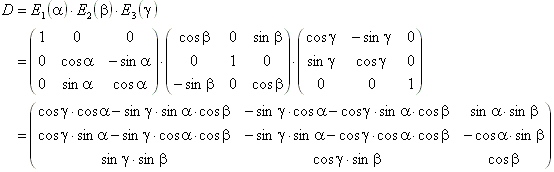
10.1.10 Beispiele für Tensoren in Physik und Technik:
Dielektrischer Tensor,
Polarisationstensor,
Trägheitstensor,
Deformationstensor,
Spannungstensor,
...
10.1.11 Koordinatendarstellung der Translation von Vektoren:
Es sei der Vektor ![]() ein fester Vektor. Dann ist die Abbildung
ein fester Vektor. Dann ist die Abbildung ![]() eine Translation (kein Tensor). Ist nun T die Koordinatendarstellung
eines Tensors in der Basis (e1, e2, e3) und T ' die Koordinatendarstellung desselben Tensors in der Basis (e1', e2', e3'), so gilt T = T '. Dies liegt an der Invarianz der
Basisvektoren bei Translation.
eine Translation (kein Tensor). Ist nun T die Koordinatendarstellung
eines Tensors in der Basis (e1, e2, e3) und T ' die Koordinatendarstellung desselben Tensors in der Basis (e1', e2', e3'), so gilt T = T '. Dies liegt an der Invarianz der
Basisvektoren bei Translation.
10.1.12 Orthogonale Transformationen:
Es sei P eine orthogonale Transformation des ![]() . Aus dem Basisvektor ej wird damit der Basisvektor ej':
. Aus dem Basisvektor ej wird damit der Basisvektor ej':
Das entstehende Koordinatensystem ist wieder orthogonal. Es gilt des weiteren:
Wenn det(P) = +1 (d.h. Drehung), dann ist (e1', e2', e3') wieder ein Rechtssystem.
10.1.12.1 Transformationsverhalten eines Vektors:
Der Vektor a bezüglich der ursprünglichen Basis (e1, e2, e3) wird nach der Transformation P zu
Hierbei ist pij eine Komponente der Transformationmatrix P.
10.1.12.2 Transformationsverhalten von Tensoren:
Ist T ein Tensor mit den Matrixkomponenten tji und P eine orthogonale Transformation des ![]() (siehe oben), ergibt sich Folgendes:
(siehe oben), ergibt sich Folgendes:
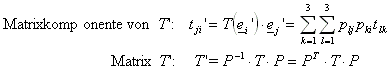
Erzeugt der Basiswechsel nicht-orthogonale Basisvektoren, so werden die Transformationformeln "etwas" komplizierter.
10.2 Das Normalformenproblem von Bilinearformen
10.2.1 Hyperfläche 2. Grades oder Quadrik:
Man definiert folgende Funktion ![]() :
:
Die hier auftretende Matrix A muß symmetrisch sein.
Die Menge der Punkte P mit ![]() , welche die Gleichung
, welche die Gleichung ![]() erfüllt, heißt Hyperfläche 2. Grades oder eine Quadrik im
erfüllt, heißt Hyperfläche 2. Grades oder eine Quadrik im ![]() .
.
Beispiel:
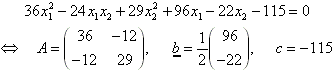
10.2.2 Mittelpunkt einer Quadrik:
Betrachtet man die Translation x = x' + p der Quadrik um p, so gilt:
Ist nun die Gleichung Ap = -b lösbar, so besitzt Q(x) ein Zentrum, für das gilt:
m heißt Mittelpunkt der Quadrik.
10.2.3 Normalform einer Quadrik:
Mit Hilfe geeigneter Koordinatentransformationen läßt sich jede Quadrik auf eine der beiden folgenden Normalformen bringen:
1. Fall:
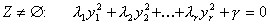
mit r = Rang(A),
Eigenwerte von A, die ungleich Null sind.
2. Fall:
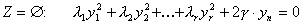
mit r = Rang(A) < n,
g > 0,
für i = 1, ..., r
10.2.4 Allgemeine Vorgehensweise bei der Klassifikation von Quadriken:
10.2.4.1 Umformungen zu Q(x):
Gegeben:
![]()
Umformungen:
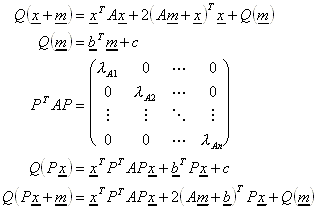
10.2.4.2 Vorgehensweise:
1. Fall: Am = -b ist lösbar. Es liegt eine Zentrumsquadrik vor.
1.) Bestimmen von m und Q(m).
2.) Bestimmen der Eigenwerte und Eigenvektoren von A. (u.U. Bestimmung des Typs)
3.) Bestimmen der Drehmatrix P aus den Eigenvektoren von A.
4.) Setze die neuen Koordinaten: ![]()
Daraus folgt
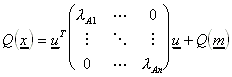
5.) Normalform (im ![]() ):
): ![]()
Typ: siehe Tabelle
Lage: Koordinatentransformation: ![]()
| l 1 | l 2 | l 3 | g | Typ |
| + | + | + | - | Ellipsoid |
| + | + | - | + | zweischaliges Hyperboloid |
| + | + | - | - | einschaliges Hyperboloid |
| + | + | - | 0 | Kegel mit Spitze in m |
| + | + | 0 | - | elliptischer Zylinder |
| + | - | 0 | +/- | hyperbolischer Zylinder |
| + | + | 0 | 0 | 1 Gerade |
| + | - | 0 | 0 | 2 Ebenen mit Schnitt |
| + | 0 | 0 | - | 2 parallele Ebenen |
| + | 0 | 0 | 0 | Doppelebene |
Tabelle 1: Klassifikation von Zentrumsquadriken
2. Fall: Am = -b ist nicht lösbar. Es liegt keine Zentrumsquadrik vor.
Es folgt daraus, daß 0 ein Eigenwert von A ist, denn det(A) = det(A - 0E) = 0
1.) Bestimmen der Eigenwerte von A.
2.) Bestimmen der Eigenvektoren v1, ..., vr zu den li 0
3.) Bestimmen der Eigenvektoren vi zu den lr+1, ..., ln-1 = 0 mit ![]()
4.) Bestimmen von vn
5.) Quadratische Ergänzung
6.) Normalform (im ![]() ):
): ![]()
Typ: siehe Tabelle
| l 1 | l 2 | l 3 | g | Typ |
| + | + | 0 | +/- | elliptisches Paraboloid |
| + | - | 0 | +/- | hyperbolisches Paraboloid |
| + | 0 | 0 | +/- | parabolischer Zylinder |
Tabelle 2: Klassifikation von Quadriken mit leerem Zentrum
10.2.4.3 Darstellung:
Die folgende Tabelle enthält nur die ersten sechs Typen von Zentrumsquadriken aus Tabelle 1 und die Typen von Quadriken mit leerem Zentrum aus Tabelle 2.
| Ellipsoid
| Zweischaliges Hyperboloid
|
| Einschaliges Hyperboloid
| Kegel mit Spitze in m
|
| Elliptischer Zylinder
| Hyperbolischer Zylinder
|
| Elliptischer Paraboloid
| Hyperbolisches Paraboloid
|
| Parabolischer Zylinder
|
Beispiel: Gesucht wird die Normalform der folgenden Quadrik.
Die Eigenwerte, die normierten Eigenvektoren und der Rang von A ergeben sich zu:
Normierte Matrix P:
Die Gleichung ![]() wird mit x = Pu zu
wird mit x = Pu zu
und nach Resubstitution ![]() ergibt sich die gesuchte Normalform der Quadrik zu
ergibt sich die gesuchte Normalform der Quadrik zu ![]() , was eine Parabel ist.
, was eine Parabel ist.
Kapitel 11: Krummlinige Koordinaten, Transformationsformel