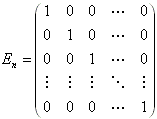
3. Matrizen, Matrixalgebra
         Kein Frame mit dem Inhaltsverzeichnis ?  => Frameset laden

3.1 Beispiele für (m,n)-Matrizen

3.1.1 (n,n)-Einheitsmatrix:

3.1.2 (m,n)-Matrix:

Der erste Index bei den Einträgen a_ij heißt Zeilenindex und gibt die Zeile an, in der der Eintrag steht, der zweite ist der Spaltenindex und gibt die Spalte der Matrix an, in der der Eintrag steht.

3.2 Rechnen mit Matrizen

3.2.1 Addition zweier (m,n)-Matrizen A und B, Multiplikation mit einer Konstanten k:

Alle Einträge werden einzeln addiert, d.h. C = A + B bzw. c_ij = a_ij + b_ij

Alle Einträge werden einzeln mit k multipliziert. C = kB bzw. c_ij = kb_ij

3.2.2 Transponieren einer (m,n)-Matrix A:

Es entsteht eine (n,m)-Matrix A^T, für deren Einträge a_jiAT gilt: a_jiAT = a_ijA

3.2.2.1 Zusatzeigenschaften bei (n,n)-Matrizen:

Eine (n,n)-Matrix A heißt symmetrisch, wenn gilt: A^T = A

Eine (n,n)-Matrix A heißt antisymmetrisch, wenn gilt: A^T = - A

Beispiel: Gegeben sind die Matrizen A und B.

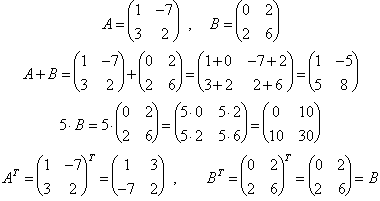
3.2.3 Verkettung von Matrizen, Matrixmultiplikation:

Generell ist dies nur möglich, wenn die erste Matrix (m,n) diesselbe Anzahl von Spalten hat wie die zweite Matrix (p,q) Zeilen, d.h. wenn n = p.

Es entsteht eine (m,q)-Matrix. Deren Einträge lauten dann allgemein:

Beispiel: Gegeben seien die beiden Matrizen A und B:

Wird A mit B verkettet, so entsteht eine (2,2)-Matrix:

Umgekehrt entsteht eine (3,3)-Matrix:

Daraus folgt: Matrixmultiplikation ist nicht kommutativ.

Aber: Multiplikation von (n,n)-Matrizen ist assoziativ, es gilt auch das Distributivgesetz.

3.2.3.1 Dyadisches Produkt:

So heißt das Produkt einer (n,1)-Matrix mit einer (1,n)-Matrix. Es ensteht eine (n,n)-Matrix.

3.2.4 Matrixinversion quadratischer Matrizen:

Es gilt für die zu A inverse Matrix A^-1: A^-1A = AA^-1 = E

Bedingung für Invertierbarkeit: det(A)0

3.2.5 Rang einer Matrix:

Unter dem Rang r(A) der (m,n)-Matrix A versteht man Folgendes: Die Maximalanzahl linear unabhängiger Zeilenvektoren (Spaltenvektoren) heißt Zeilenrang (Spaltenrang) der Matrix A. Zeilenregulär ist die Matrix A, wenn r(A) = m, spaltenregulär, wenn r(A) = n.

Eine (n,n)-Matrix heißt regulär, wenn r(A) = n und singulär, wenn r(A) < n.

Die Existenz der Inversen A^-1 und die Regularität von A sind äquivalent.

Zur Berechnung des Ranges einer (m,n)-Matrix werden die größtmöglichen Unterdeterminanten gebildet. Ist eine von ihnen nicht null, so ist der Rang gleich der Ordnung (Anzahl der Spaltenvektoren) dieser Unterdeterminante. Gegebenenfalls muß die Ordnung der Unterdeter-minante verringert werden, bis eine von ihnen ungleich null ist.

3.2.6 Lösung einfacher Matrixgleichungen:

Die Gleichung AX = B hat die Lösung X = BA^-1.

Dies setzt die Existens der inversen Matrix A^-1 voraus.

3.2.7 Rechenregeln für Determinanten:

det(A B) = det(A) det(B) (Produktregel)

det(A^T) = det(A)

det(E_n) = 1

det(c A) = cⁿ det(A)     für (n,n)-Matrizen

3.3 Eigenwerte und Eigenvektoren

Gegeben sei eine lineare Abbildung

Unter den Eigenwerten l und den Eigenvektoren der Matrix A versteht man alle diejenigen Konstanten bzw. Vektoren, für die gilt:

Aus dieser Definition folgt:

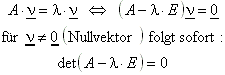
In Determinantenschreibweise:

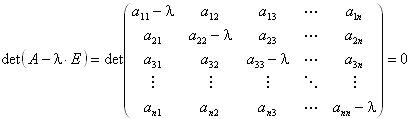
Beispiel: Gesucht sind alle Eigenwerte und Eigenvektoren der Matrix A:

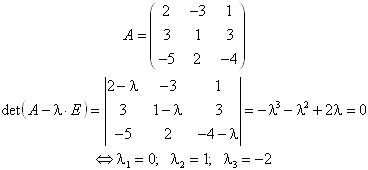
Die einzelnen Eigenwerte werden in das jeweilige (überbestimmte) homogene Gleichungssystem eingesetzt und dessen Lösungsmenge nach bekannten Verfahren bestimmt. Diese ist dann der zum einzelnen Eigenwert gehörende Eigenvektor. In der Regel werden die Eigenvektoren auf den Betrag 1 normiert.

Ein Spezialfall ergibt sich, wenn außer der Hauptdiagonalen der Matrix nur Nullen in ihr stehen. Die Zahlen in der Hauptdiagonalen sind dann zugleich die Eigenwerte der Matrix.

Kapitel 4: Folgen und Reihen