Kapitel 4: Folgen und Reihen

4. Folgen und Reihen
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset laden

4.1 Folgen

4.1.1 Teilfolge:

Unter einer Teilfolge versteht man eine Folge, die durch Wegstreichen von bestimmten Gliedern aus einer anderen Folge, aber ohne Veränderung der Reihenfolge, aus jener Folge entsteht.

4.1.2 Konvergenz:

Eine Folge oder Reihe konvergiert, wenn die Differenz zwischen einem Folgenglied (bzw. die Folge der Partialsummen der Reihe) und dem zugehörigen Grenzwert jeden beliebigen reellen Wert unterschreiten kann:

4.1.3 Divergenz:

Eine nicht konvergente Folge (oder Reihe) heißt divergent. Sie heißt bestimmt divergent, wenn gilt:

4.1.4 Beschränkte Folgen:

Eine Folge heißt beschränkt, wenn es eine positive reelle Zahl gibt, die gegenüber dem einzelnen Absolutbetrag jedes einzelnen Folgengliedes immer größer (oder gleich) ist. Sie ist nach unten beschränkt, wenn der Absolutbetrag |a| = -a ist und nach oben beschränkt, wenn |a| = a ist. Eine Vektorfolge heißt beschränkt, wenn der Betrag der Folgenvektoren beschränkt ist. Dies wiederum ist der Fall, wenn jede Kompnentenfolge beschränkt ist.

4.1.5 Monotonie:

Wenn alle k sind, kann für Folgen formuliert werden:

4.1.6 Eulersche Zahl:

Die Eulersche Zahl e ist der Grenzwert einer Folge:

4.1.7 Konvergenzkriterium von CAUCHY:

Satz und Definition: Eine reelle oder komplexe Folge bzw. Vektorfolge ist genau dann konvergent, wenn sie eine Cauchy-Folge ist, d.h. es gibt zum eine Zahl , für die existiert

4.1.8 Rekursiv definierte Folgen:

Die Folgenglieder werden mit Hilfe des vorherigen bestimmt, z.B.:

4.1.9 Regeln bei Grenzwertbestimmungen:

4.1.10 Alternierende Folgen:

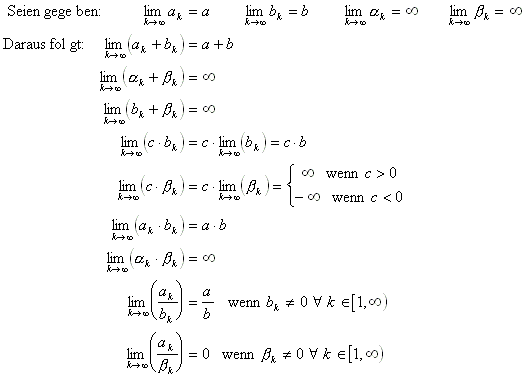
Folgen, die mit jedem Folgenglied zwischen positiven und negativen Werten schwanken, heißen alternierende Folgen.

Beispiel:

4.2 Unendliche Reihen

Wird einer unendlichen Folge von Zahlen eine Summe zugeordnet, die als Summanden die Folgenglieder haben, so heißt diese Summe unendliche Reihe. Werden nur die Folgenglieder bis zur Stelle k addiert, so spricht man von der k-ten Partialsumme der Reihe. Die Konvergenz, Divergenz und Monotonie wird definiert wie bei Folgen.

4.2.1 CAUCHY-Kriterium für Reihen:

Es besagt analog zum Cauchy-Kriterium für Folgen, daß es zu jeder Differenz zweier Partialsummen m und n, welche kleiner als ein ist, ein gibt, für das gilt: . Allgemein muß gelten, daß die Folge der Partialsummen konvergiert.

Beispiel: Die harmonische Reihe ist divergent.

Erfüllt eine Reihe das Cauchy-Kriterium, so gilt:

4.2.2 Majoranten- und Minorantenkriterium:

Mit der Reihe , läßt sich sagen:

4.2.2.1 Die konvergente Reihe heißt Majorantenreihe von , wenn ab einer bestimmten Stelle N0 das Reihenglied bk ständig größer ist als |ak|. Dann ist die Reihe absolut konvergent.

4.2.2.2 Die divergente Reihe heißt Minorantenreihe von , wenn ab einer bestimmten Stelle N0 das Reihenglied ck ständig kleiner ist als |ak|. Dann ist die Reihe 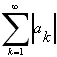divergent (die Reihe nicht absolut konvergent).