11. Krummlinige Koordinaten, Transformationsformel
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
11.1 Krummlinige Koordinaten, Jacobideterminante
11.1.1 Krummlinige Koordinaten:
Gegeben seien drei Eckpunkte eines zu den Koordinatenachsen parallelen Rechtecks im ![]() durch deren Ortvektoren:
durch deren Ortvektoren:
Die Verzerrung des Rechtecks mit dem Flächeninhalt ![]() in ein Parallelogramm, dargestellt durch die neuen Eckpunkte
in ein Parallelogramm, dargestellt durch die neuen Eckpunkte
,
mit der Funktion f ergibt für den Grenzwert der Verhältnisse zwischen dem ursprünglichen Flächeninhalt FQ und dem neuen Flächeninhalt FP Folgendes:
Diese Flächenverzerrung im zweidimensionalen Raum läßt sich analog übertragen auf Gebilde im ![]() . Dort stellt sie die Volumenverzerrung im
dreidimensionalen Raum dar.
. Dort stellt sie die Volumenverzerrung im
dreidimensionalen Raum dar.
11.1.1.1 Wird bei solchen Verzerrungen kein begrenztes Objekt betrachtet, sondern eine offene Menge U in eine offene Menge V verzerrt, so spricht man bei f von der Koordinatentransformation von U auf V.
11.1.1.2 Zur Umkehrung einer solchen Koordinatentransformation läßt sich unter der Voraussetzung, daß ![]() , Folgendes sagen:
, Folgendes sagen:
In diesem Zusammenhang wird der Begriff der Funktionaldeterminante oder Jacobideterminante eingeführt.
Koordinatentransformation:
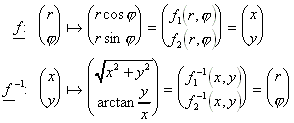
Jacobideterminante von f:
![]()
Koordinatentransformation:
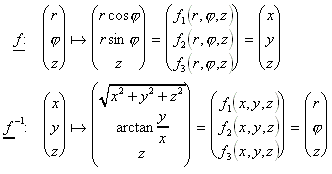
Jacobideterminante von f:
![]()
Koordinatentransformation:
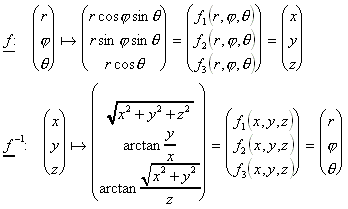
Hierbei liegt der Winkel j zwischen der x-Achse und dem in die x-y-Ebene projizierten Ortsvektor des Punktes. Der Winkel q liegt zwischen der
z-Achse und dem Ortsvektor des Punktes.
Jacobideterminante von f:
![]()
Für eine zweifach differenzierbare Funktion ![]() von
von ![]() auf
auf ![]() läßt sich der sog. Laplace-Operator D definieren:
läßt sich der sog. Laplace-Operator D definieren:
![]()
Bei Koordinatentransformationen ![]() zwischen offenen, nichtleeren Mengen U und V, mit meßbarem
zwischen offenen, nichtleeren Mengen U und V, mit meßbarem ![]() und stetigem
und stetigem ![]() gilt die
Transformationsformel.
gilt die
Transformationsformel.
![]()
Beispiel: Gesucht wird das neue Volumen Vol(B) eines Parallelepipeds B, das durch eine affin-lineare Abbildung u = Ax + b eines Einheitswürfels W entstanden ist.
Aus ![]() ,
, ![]() und der Transformationsformel
und der Transformationsformel
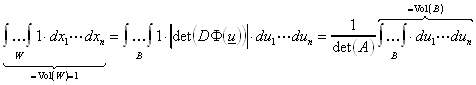 folgt dann:
folgt dann:
Kapitel 12: Gewöhnliche Differentialgleichungen