12. Gewöhnliche Differentialgleichungen
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
12.1 Bezeichnungen, Richtungsfeld
12.1.1 Gewöhnliche Differentialgleichung:
F sei eine Funktion der Form ![]() . Dann heißt
. Dann heißt
![]()
gewöhnliche Differentialgleichung.
12.1.2 Richtungsfeld, Isokline:
Wenn durch den Punkt M die Lösungskurve ![]() der Differentialgleichung
der Differentialgleichung ![]() geht, so kann die Richtung der Tangente in diesem Punkt
unmittelbar ermittelt werden. Damit definiert die Differentialgleichung in jedem Punkt eine Richtung der Tangente an eine Lösungskurve. Die Gesamtheit dieser
Richtungen bildet das Richtungsfeld. Verbindungslinien von Punkten gleicher Richtung der Tangente heißen Isoklinen.
geht, so kann die Richtung der Tangente in diesem Punkt
unmittelbar ermittelt werden. Damit definiert die Differentialgleichung in jedem Punkt eine Richtung der Tangente an eine Lösungskurve. Die Gesamtheit dieser
Richtungen bildet das Richtungsfeld. Verbindungslinien von Punkten gleicher Richtung der Tangente heißen Isoklinen.
Die Lösungen von gewöhnlichen Differentialgleichung mit einer Anfangsbedingung setzen sich in der Regel aus der Summe von mindestens zwei Einzellösungen zusammen. Die Lösung einer allgemeinen Differentialgleichung ist dann die Summe der homogenen Lösung und der inhomogenen oder partikulären Lösung.
Erhält man aus einer Differentialgleichung eine Lösungsmenge, so ist jede Linearkombination von Einzellösungen wieder eine Lösung. Dies ist mit dem Faktorsatz
und der Summenregel aus der Differentialrechnung erklärbar (Kapitel 6.1).
12.1.4 Anfangswertproblem (AWP):
Als Anfangswertproblem bezeichnet man eine Differentialgleichung zusammen mit ihren zugehörigen Anfangsbedingungen.
12.1.5 Satz von Picard-Lindelöf:
Es sei ein Anfangswertproblem ![]() ,
, ![]() gegeben. Ferner sei ein Rechteck
gegeben. Ferner sei ein Rechteck
![]()
gegeben, auf dem die Funktion f(x,y) stetig und partiell nach y differenzierbar sei.
Eine Zahl e sei durch 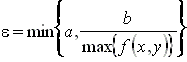 bestimmt.
bestimmt.
Es gibt dann im Abstand e von x0 genau eine Lösung zum gegebenen Anfangswertproblem.
12.2 Differentialgleichungen erster Ordnung
12.2.1 Form, Anfangsbedingung:
Differentialgleichungen erster Ordnung besitzen die Form ![]() .
.
Es seien hier A(x) und B(x) im Intervall [a,b] stetig. Des weiteren sollen ein x0 aus dem gegebenen Intervall und ein (reelles) y0 existieren, die die
Anfangsbedingung ![]() bilden.
bilden.
12.2.2 Homogene Differentialgleichung:
Ist A(x)=0, also ![]() , so hat diese als homogen bezeichnete Differentialgleichung genau eine Lösung der allgemeinen Form
, so hat diese als homogen bezeichnete Differentialgleichung genau eine Lösung der allgemeinen Form
![]() .
.
Diese Lösungsfunktion ist immer positiv.
12.2.3 Inhomogene Differentialgleichung:
Differentialgleichungen erster Ordnung in der allgemeinen Form und allgemeinen Anfangsbedingungen (s. 12.2.1) haben die partikuläre Lösung in der Form
.
Die allgemeine Lösung lautet:
12.2.5 Trennung der Variablen:
Ein wichtiges Verfahren zur Lösung von Differentialgleichungen erster Ordnung ist das der Trennung der Variablen. Dabei wird die Differentialgleichung auf eine
Form gebracht, bei der die Variablen x und y nur noch in voneinander getrennten Termen auftreten. Die entstehende Gleichung kann dann sofort integriert werden.
Beispiel:
12.3 Bernoulli'sche Differentialgleichungen
Bernoulli'sche Differentialgleichungen haben die Form
![]() .
.
Ziel dieses Ansatzes ist die Rückführung der Differentialgleichung auf eine Differentialgleichung erster Ordnung. Es wird zunächst durch durch ![]() geteilt.
geteilt.
![]()
Danach wird die neue Variable ![]() eingeführt.
eingeführt.
Deren Ableitung lautet ![]() . Es ergibt sich daraus eine Differentialgleichung erster Ordnung für z(x):
. Es ergibt sich daraus eine Differentialgleichung erster Ordnung für z(x):
![]()
Diese DGL läßt sich mit dem in Kapitel 12.2 beschriebenen Verfahren lösen. Anschließend wird mit ![]() resubstituiert.
resubstituiert.
Beispiel: Gesucht wird die allgemeine Lösung der folgenden Differentialgleichung.
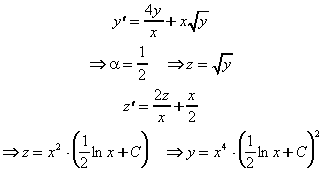
12.4 Differentialgleichungen n-ter Ordnung und Systeme erster Ordnung
12.4.1 Form von Systemen von Differentialgleichungen erster Ordnung:
Komponentenschreibweise:
Vektorschreibweise: ![]()
Anfangswertproblem: ![]()
12.4.2 Form von Differentialgleichungen n-ter Ordnung:
Differentialgleichungen n-ter Ordnung werden geschrieben in der Form
![]() .
.
Es wird eine Substitution durchgeführt.
Daraus folgen das neue System von Differentialgleichungen und die neuen Anfangsbedingungen.
Die allgemeine Lösung einer Differentialgleichung der Form ![]() enthält n unabhängige willkürliche Konstanten.
enthält n unabhängige willkürliche Konstanten.
Das gleiche gilt für die allgemeine Lösung von Systemen von n Differentialgleichungen.
Das Lösungsprinzip beruht darauf, daß versucht wird, die Ordnung mittels Substitution der Variablen zu erniedrigen, um einfachere Differentialgleichungen zu
erhalten. Das Auffinden passender Substitutionen wird erleichtert durch die Unterscheidung verschiedener Fälle:
1. Die unabhängige Variable x ist nicht explizit in der Differentialgleichung enthalten.
Die Substitution lautet dann ![]() .
.
Damit wird die Ordnung von n auf (n-1) verringert.
2. Die abhängige Variable y ist nicht explizit in der Differentialgleichung enthalten.
Die Substitution lautet ![]() für die k-te als niedrigste in der Differentialgleichung
für die k-te als niedrigste in der Differentialgleichung
vorkommende Ableitung von y. Die Ordnung der DGL wird damit um eins verringert.
3. Die Differentialgleichung ![]() ist eine homogene Funktion in
ist eine homogene Funktion in ![]() .
.
Die Substitution lautet ![]() .
.
Die Ordnung wird um eins erniedrigt.
4. Die Differentialgleichung ist eine Funktion nur von x.
Die allgemeine Lösung lautet dann folgendermaßen:
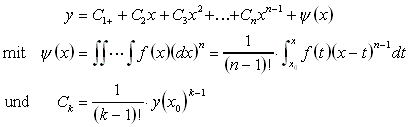
Hilfreich kann bei der Lösung solcher Differentialgleichungen auch die folgende Beziehung sein:
![]()
Genaueres zu derartigen Differentialgleichungen befindet sich im Bronstein / Semendjajew / Musiol / Mühlig: Taschenbuch der Mathematik (1. Auflage,
1993) auf den Seiten 330 bis 333.
12.5 Lineare Differentialgleichungs-Systeme erster Ordnung
12.5.1 Lineares Differentialgleichungs-System erster Ordnung:
Es hat die folgende Form:
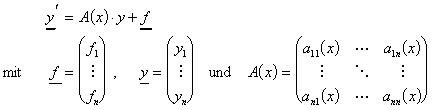
Ist ![]() , so heißt das System homogen, sonst inhomogen.
, so heißt das System homogen, sonst inhomogen.
Ist A eine konstante Matrix, so spricht man von einem System mit konstanten Koeffizienten.
Mit Ausnahme der Unterpunkte 12.5.1 bis 12.5.3 sollen nur DGL-Systeme mit konstanten Matrizen behandelt werden.
12.5.1.1 Lösbarkeit:
Sind die Elemente aik(x) der Matrix und die Funktion f stetig in einem gegebenen Intervall, so hat das DGL-System genau eine Lösung in diesem Intervall.
12.5.1.2 Linearkombinationen von Lösungen eines homogenen linearen DGL-Systems:
Sind y1,...,yk Lösungen eines homogenen linearen DGL-Systems, dann ist auch jede beliebige Linearkombination ![]() von Lösungen wieder eine neue Lösung.
von Lösungen wieder eine neue Lösung.
12.5.2 Lineare Abhängigkeit, lineare Unabhängigkeit von Lösungen:
Die Funktionen y1,...,yk nennt man auf einem Intervall linear unabhängig, falls für alle x aus diesem Intervall aus
![]() folgt.
folgt.
Andernfalls heißen y1,...,yk linear abhängig.
12.5.3 Anzahl linear unabhängiger Lösungen:
Ist die Matrix ![]() stetig in einem Intervall für x, dann hat das System
stetig in einem Intervall für x, dann hat das System ![]() genau n linear unabhängige Lösungen in diesem Intervall.
genau n linear unabhängige Lösungen in diesem Intervall.
12.5.4 Fundamentalsystem (FS), Fundamentalmatrix, Übertragungsmatrix:
12.5.4.1 Fundamentalsystem:
Ein System y1,...,yn linear unabhängiger Lösungen von ![]() heißt Fundamentalsystem.
heißt Fundamentalsystem.
12.5.4.2 Fundamentalmatrix:
Als Fundamentalmatrix bezeichnet man die Matrix ![]() .
.
Die reell gewählte Fundamentalmatrix ermöglicht später die direkte Berechnung eines homogenen Lösungsanteils:
![]()
Eigenschaften der Fundamentalmatrix:
1. ![]()
2. ![]()
12.5.4.3 Übertragungsmatrix oder normierte Matrix:
Die (stets reelle) Übertragungsmatrix lautet: ![]()
Homogener Lösungsanteil des DGL-Systems, berechnet mit der Übertragungsmatrix:
![]()
Eigenschaften der Übertragungsmatrix:
1.
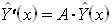
2.
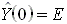
3.
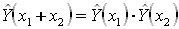
4.
12.5.5 Wronski-Determinante eines homogenen linearen DGL-Systems:
Haben die Lösungen y1,...,yn die Dimension n, so wird
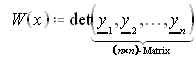
Wronski-Determinante genannt.
Ist die Wronski-Determinante W(x) ¹ 0 für alle x, so bilden die Lösungen y1,...,yn ein Fundamentalsystem. Für lineare Differentialgleichungen n-ter
Ordnung wird die Wronski-Determinante etwas anders definiert.
12.5.6 Lösungsverfahren für lineare Differentialgleichungs-Systeme erster Ordnung:
Die allgemeine Lösung setzt sich zusammen aus einem homogenen Lösungsanteil und einem partikulären Lösungsanteil.
![]()
12.5.6.1 Bestimmung des homogenen Lösungsanteils:
1. Schritt: Die homogenen linearen DGL-Systeme ![]() werden mit Hilfe der Eigenvektoren und der Eigenwerte der Matrix A gelöst. Aus der
Charakteristischen Gleichung
werden mit Hilfe der Eigenvektoren und der Eigenwerte der Matrix A gelöst. Aus der
Charakteristischen Gleichung
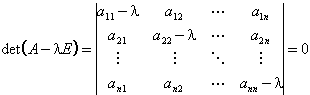
erhält man ein vollständiges System von (komplexen) Wurzeln l1, l2, ..., ln (Eigenwerte von A).
2. Schritt: Danach sind zwei Fälle zu unterscheiden.
1. Fall: Verschiedene Wurzeln li
Mit der Gleichung
![]()
erhält man für jede der Wurzeln li je einen Lösungsvektor ni , der nicht normiert werden muß.
Das (komplexe) Fundamentalsystem ergibt sich dann zu Folgendem:
FS:
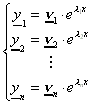
Tritt in dem vollständigen System der Wurzeln eine komplexe Wurzel auf (z.B. ![]() ), dann kommt in dem System auch die konjugiert-komplexe Wurzel
), dann kommt in dem System auch die konjugiert-komplexe Wurzel
![]() vor.
vor.
Daraus folgt dann, daß auch die zugehörigen Lösungsvektoren konjugiert-komplex sind.
Diese beiden komplexen Lösungen können durch zwei reelle Lösungsvektoren ersetzt werden. Sie lauten folgendermaßen:
Die beiden Vektoren entsprechen dem Real- bzw. dem Imaginärteil von y1.
Beispiel: Gesucht wird die allgemeine Lösung des folgenden DGL-Systems.
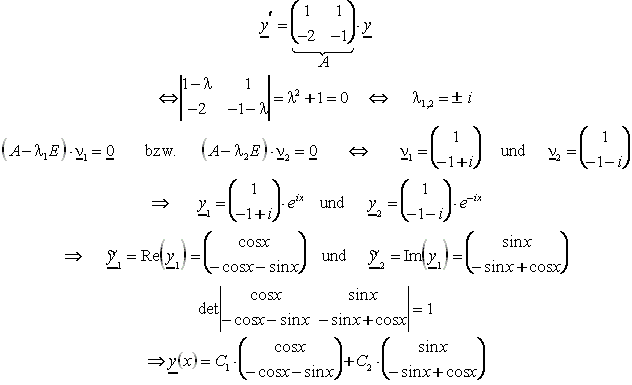
2. Fall: Mehrfache Wurzeln li
Die Wurzel li trete r-mal auf. Die Lösungen, die der r-fachen Wurzel li im Fundamentalsystem entsprechen, erhält man mit dem Ansatz
![]() .
.
Das auftretende Polynom ist vom Grad r-1. Die Vektoren ui sind unbestimmt. Setzt man nun yi in das DGL-System ein, so entsteht ein lineares Gleichungssystem
für die Vektorkoordinaten, von denen r entsprechend der Vielfachheiten der Wurzel li beliebig wählbar sind.
Beispiel: Gesucht wird die allgemeine Lösung des folgenden DGL-Systems.
Der einfachen Wurzel l1 = 0 entspricht der Lösungsansatz:
.
Einsetzen in das DGL-System ergibt
Die Vielfachheit der Wurzel l2,3 ist zwei, der zu benutzende Ansatz lautet dann:
Einsetzen in das DGL-System und Auflösen des linearen Gleichungssystems führt auf:
Die Fundamentallösungen zu l2,3 = 1 lauten dann:
Sie bilden zusammen mit y1 ein Fundamentalsystem. Die allgemeine Lösung lautet:
Im allgemeinen Fall, d.h. unabhängig von der Vielfachheit der Eigenwerte der Matrix A ist das folgende Lösungsprinzip anwendbar. Es ist dem hier schon
beschriebenen Verfahren äquivalent.
Lösungsprinzip unter Verwendung der Übertragungsmatrix:
Nach der Bestimmung der Übertragungsmatrix aus dem Fundamentalsystem gemäß der Formel
ergibt sich die homogene, reelle Lösung des vorgegebenen Anfangswertproblems zu Folgendem:
Mehr zu den Eigenschaften der Übertragungsmatrix befindet sich unter Punkt 12.5.4.3 .
12.5.6.2 Bestimmung des partikulären Lösungsanteils:
1. Schritt: Für das Störglied f(x) des DGL-Systems ![]() wird folgender Ansatz gemacht:
wird folgender Ansatz gemacht:
![]()
Die Zahlen b und ![]() müssen reell sein,
müssen reell sein, ![]() darf kein Eigenwert von A sein.
darf kein Eigenwert von A sein.
q1(x) und q2(x) sind reelle Vektorpolynome.
Ist m ein Eigenwert, so wird im 3. Schritt eine kleine Änderung vorgenommen.
2. Schritt: Man bildet dann die sogenannte komplexe Störfunktion:
![]()
3. Schritt: Der nächste Ansatz lautet:
![]()
Fall m ein Eigenwert ist, so wird dieser Ansatz gemacht:
![]()
Dies erzeugt zwar später ein Gleichungssystem höherer Ordnung, sonst müßte aber eine Fallunterscheidung für die Funktionswerte von m im
charakteristischen Polynom vorgenommen werden, die etwas mehr Zeit beansprucht.
4. Schritt: Dieser Ansatz für die partikuläre Lösung wird in das DGL-System eingesetzt.
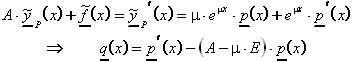
Die letzte Gleichung lassen sich die Koeffizienten von p(x) ermitteln.
Damit erhält man die partikuläre Lösung ![]() .
.
Beispiel: Gesucht ist eine partikuläre Lösung des folgenden DGL-Systems.
![]()
Nach dem ersten Ansatz folgt:
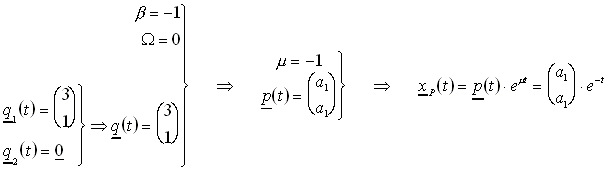
Im nächsten Schritt wird nun dieser Lösungsansatz in das DGL-System eingesetzt und die unbekannten Koeffizienten ermittelt.
Lösungsprinzip unter Verwendung der Übertragungsmatrix:
Auch die partikuläre Lösung läßt sich mit Hilfe der Übertragungsmatrix ermitteln. Sie lautet allgemein:
Zur Berechnung des Vektors c(x) sind in der Regel etwas ausgefallenere Integrale zu lösen.
Beispiel: Gesucht wird eine partikuläre Lösung zum folgenden DGL-System, dessen Übertragungsmatrix bereits bestimmt wurde.
Nach der obenstehenden Formel ergibt sich dann:
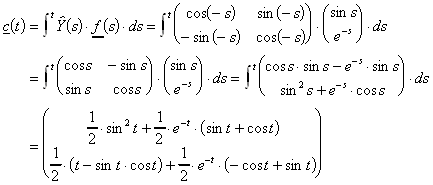
Die partikuläre Lösung lautet:
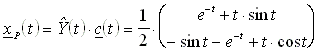
12.5.7 Allgemeine Lösung eines gegebenen Anfangswertproblems:
Faßt man alle bis hierher gewonnenen Erkenntnisse zusammen, so ergibt sich folgende Formel:
Ausgedrückt mit der Übertragungmatrix:
12.6 Lineare Differentialgleichungen n-ter Ordnung
12.6.1 Lineare Differentialgleichung n-ter Ordnung:
Unter einer linearen Differentialgleichung n-ter Ordnung versteht man eine Differentialgleichung der Form
![]() .
.
Diese heißt homogen, falls f(x) = 0 ist, sie heißt inhomogen, falls f(x) ¹ 0 ist.
12.6.1.1 Lösbarkeit:
Sind die Koeffizienten ak(x) und f(x) stetig in einem gegebenen Intervall, so hat für ein x0 aus diesem Intervall das Anfangswertproblem
mit reellen yk genau eine Lösung im gegebenen Intervall.
Im Folgenden sollen nur Differentialgleichungen mit konstanten Koeffizienten betrachtet werden.
12.5.1.2 Linearkombinationen von Lösungen einer linearen DGL n-ter Ordnung:
Sind y1,...,yk Lösungen einer homogenen linearen DGL n-ter Ordnung, dann ist auch jede beliebige Linearkombination
![]() von Lösungen wieder eine neue Lösung.
von Lösungen wieder eine neue Lösung.
12.6.2 Umformung in DGL-System erster Ordnung:
Es werden Substitutionen durchgeführt:
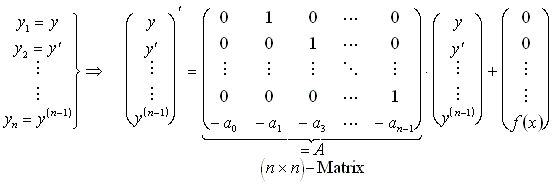
Die Darstellung des Fundamentalsystems von Lösungen sieht folgendermaßen aus:
12.6.4 Aufstellen eines Fundamentalsystems:
Gegeben ist die homogene lineare DGL n-ter Ordnung mit konstanten Koeffizienten:
![]()
Man erhält ein Fundamentalsystem, wenn man zu jeder r-fachen Nullstelle lk die rk Lösungen
![]()
und zu jedem Paar konjugiert-komplexer Nullstellen ![]() (r-fach) die 2r Lösungen
(r-fach) die 2r Lösungen
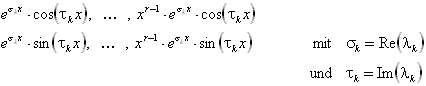
zusammenfaßt.
12.6.5 Fundamentalmatrix, Übertragungsmatrix:
Sie wird ebenso aufgestellt wie bei normalen DGL-Systemen:
Sie besitzt alle bereits bei DGL-Systemen beschriebenen Eigenschaften (s. Punkt 12.5.4.3).
Das Aufstellen der Übertragungsmatrix erfolgt entsprechend.
Analog zu DGL-Systemen lautet sie:
Ist der Betrag der Wronski-Determinante nicht null, so bilden die Spaltenvektoren ein Fundamentalsystem zur gegebenen Differentialgleichung.
12.6.7 Allgemeines Lösungsverfahren:
12.6.7.1 Charakteristisches Polynom:
Zur Differentialgleichung ![]() wird das charakteristische Polynom oder charakteristische Gleichung
folgendermaßen definiert:
wird das charakteristische Polynom oder charakteristische Gleichung
folgendermaßen definiert:
![]()
12.6.7.2 Bestimmung des homogenen Lösungsanteils:
1.Schritt: Zuerst werden die Nullstellen der charakteristischen Gleichung ermittelt.
2. Schritt: Danach wird das reelle Fundamentalsystem aufgestellt.
3. Schritt: Die Lösung des homogenen DGL-Anteils lautet dann:
12.6.7.3 Bestimmung des partikulären Lösungsanteils:
1. Schritt: Für das Störglied f(x) der DGL wird folgender Ansatz gemacht:
Die Zahlen b und ![]() müssen reell sein. q1(x) und q2(x) sind reelle Polynome.
müssen reell sein. q1(x) und q2(x) sind reelle Polynome.
2. Schritt: Man bildet dann die sogenannte komplexe Störfunktion:
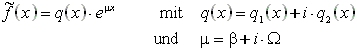
3. Schritt: Der nächste Ansatz lautet:
![]()
Die partikuläre (komplexe) Lösung wird wie folgt angesetzt: ![]()
Daraus folgt dann:
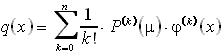
Im Falle, daß die Differentialgleichung zweiter Ordnung ist, gilt vereinfacht:
![]() mit
mit ![]()
4. Schritt: Aus der obenstehenden Formel werden schrittweise alle Koeffizienten bestimmt. Dazu
kann der Koeffizientenvergleich - d.h. Vergleich von Real- bzw. Imaginärteilen auf beiden
Seiten der Gleichung - angewandt werden.
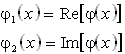
Daraus folgt schließlich für die partikuläre Lösung:
![]()
Beispiel: Gesucht wird die allgemeine Lösung der folgenden linearen Differentialgleichung.
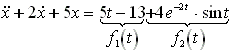
Eine solche Aufteilung des Störgliedes in zwei (oder mehr) Teile wird dann notwendig, wenn es offensichtlich nicht die allgemeine Form
![]() von Störgliedern besitzt.
von Störgliedern besitzt.
Homogene Lösung:
Es werden die Nullstellen des charakteristischen Polynoms P(l) bestimmt.
![]()
Die allgemeine, reelle Lösung der homogenen Differentialgleichung lautet dann:
![]()
Partikuläre Lösung:
Zu f1(t):
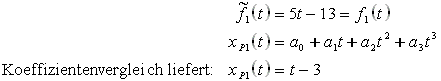
Zu f2(t):
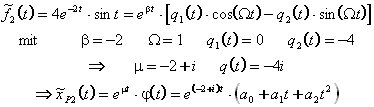
Als nächstes wird der Ansatz ![]() benutzt, um die unbekannten Koeffizienten von j(t) zu bestimmen. Diese
ergeben sich zu Folgendem:
benutzt, um die unbekannten Koeffizienten von j(t) zu bestimmen. Diese
ergeben sich zu Folgendem:
Die allgemeine Lösung des zweiten Teils vom Störglied lautet dann:
![]()
Die allgemeine Lösung der gesamten Differentialgleichung ergibt sich somit zu:
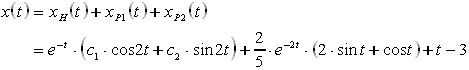
12.6.8 Tabelle zur Lösungsbasis von linearen homogenen Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten:
Die homogene Lösung lautet ![]() mit y1(x) und y2(x) aus der untenstehenden Tabelle.
mit y1(x) und y2(x) aus der untenstehenden Tabelle.
| Nullstellen von P(l) | Lösungsbasis der Differentialgleichung |
12.7 Eulersche Differentialgleichungen
12.7.1 Form Eulerscher Differentialgleichungen
Allgemein sehen diese Differentialgleichung folgendermaßen aus:
![]()
12.7.2 Allgemeines Löungsverfahren:
Es wird eine Substitution durchgeführt, die aus dieser speziellen Differentialgleichung eine lineare Differentialgleichung mit konstanten Koeffizienten macht.
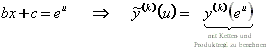
Die Resubstitution lautet dann: ![]()
12.7.3 Spezielle Eulersche Differentialgleichung zweiter Ordnung:
In der Form
![]()
vereinfacht sich die Substitution auf
![]()
und die neue Differentialgleichung lautet:
![]()
12.8 Rand- und Eigenwertprobleme
12.8.1 Begriff des Randwertproblems (RWP):
Unter Randwertproblemen versteht man Probleme, bei denen die gesuchte Lösung einer Differentialgleichung (eines DGL-Systems) in der Endpunkten eines
Intervalls der unabhänigen Variable(n) bei vorgegebenen Bedingungen genügen muß. Randwertprobleme treten in der Physik sehr häufig auf.
Gegeben sei L[y] = f(x), eine lineare Differentialgleichung n-ter Ordnung mit auf [a,b] stetigen Koeffizienten. f(x) sei ebenfalls stetig. Die Randbedingungen seien
![]()
und g1, ..., gm reell.
Dann bestimmen die Gleichungen
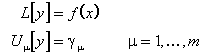
ein Randwertproblem (RWP).
12.8.2 Begriff des Eigenwertproblems bei Differentialgleichungen:
Analog zur Definition des Eigenwertproblems bei Matrizen wird festgelegt:
![]()
heißt Eigenwertproblem der Differentialgleichung L[y]. l heißt Eigenwert zur Eigenfunktion y, die diese Gleichung unter gegebenen Randbedingungen erfüllt.
In den meisten Fällen muß für l eine Fallunterscheidung durchgeführt werden.
Beispiel: Bestimmt werden sollen die Eigenwerte und die Eigenfunktionen des Randwertproblems
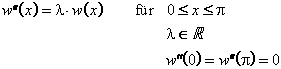
1. Fall: l > 0: Die allgemeine Lösung der DGL lautet dann ![]() .
.
Koeffizientenvergleich nach Einsetzen in die DGL liefert:
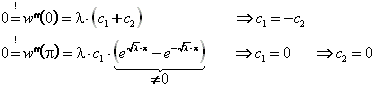
Die erhaltene Lösung für l > 0 ist also die triviale Lösung ![]() .
.
2. Fall: l = 0: Die Lösung der entstehenden DGL ![]() lautet
lautet ![]() ,
,
d.h., Eigenfunktionen zum Eigenwert l = 0 sind w(x) = x und w(x) = 1.
3. Fall: l < 0: In diesem Fall lautet die allgemeine Lösung:
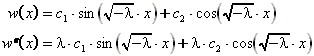
Durch Koeffizientenvergleich ergibt sich:
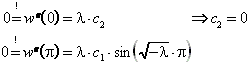
Da l 0 ist, muß entweder c1 = 0 (triviale Lösung) oder l = -n² sein (n ganzzahlig). Zugehörige Eigenfunktionen sind
![]() .
.
12.9 Autonome Differentialgleichungen 2. Ordnung
In der allgemeinen Form lauten sie:
![]()
Die unabhängige Variable t kommt nicht explizit vor.
Anfangswerte: ![]()
12.9.2 Äquivalentes DGL-System erster Ordnung:
Es wird geschieben in der Form:
![]()
Die Anfangswerte lauten dann: ![]()
In Anlehnung an die Physik wird p als Impuls bezeichnet, f sei ein Kraftfeld in einem bestimmten Gebiet der (x,p)-Phasenebene (Orts-Impuls-Ebene).
(xs,ps) heißt singulärer Punkt (SP) der Differentialgleichung ![]() , wenn folgendes gilt:
, wenn folgendes gilt:
![]()
Die singulären Punkte liegen auf der x-Achse. Andere Bezeichnungen für singuläre Punkte sind Gleichgewichtslage oder Ruhelage der Differentialgleichung.
Eine orientierte Kurve G in der (x,p)-Ebene heißt Phasenkurve (PK) der Differentialgleichung ![]() , wenn es eine Lösung
, wenn es eine Lösung
![]()
gibt, die eine Parameterdarstellung (PD) von G ist.
Merkregel für die Pfeilrichtung:
Die Pfeile weisen nach rechts, wenn p positiv ist. Wenn p negativ ist, weisen die Pfeile nach links.
12.9.5 Bestimmung der Phasenkurve, Lösen von Anfangswertproblemen:
Die Bestimmung erfolgt in mehreren Schritten.
1. Schritt: Ansatz für G mit (x0,p0) G :
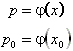
Gesucht ist j(x).
Nach einigen Umformungen und Substitutionen ergibt sich:
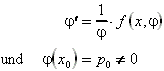
Dies ist eine Differentialgleichung erster Ordnung für j(x).
2. Schritt: j(x) wird berechnet.
Man löst eine Differentialgleichung erster Ordnung für x(t), indem man
![]()
einsetzt. Es ergibt sich das Folgende:
![]()
Daraus erhält man t als Funktion von x. Aufgelöst nach x(t) hat man dann die Parameterdarstellung der Phasenkurve durch (x0,p0).
Beispiel: Gesucht ist die Lösung des folgenden Anfangswertproblems:
![]()
Substitution ergibt:
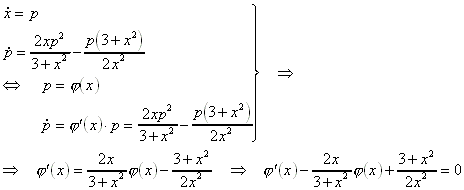
Nach Lösungsformel für Differentialgleichungen erster Ordnung ergibt sich:
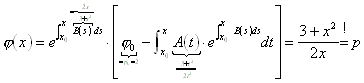
Damit ist die Phasenkurve bestimmt. Weiter kann berechnet werden:
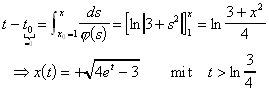
Dies ist die Lösung des angegebenen Anfangswertproblems.
12.9.6 Spezielle autonome Differentialgleichungen 2. Ordnung:
Wenn sich die Differentialgleichung schreiben läßt als
![]() ,
,
dann lassen sich ein Potential (potentielle Energie), kinetische Energie und Gesamtenergie einer Masse m = 1 definieren.
12.9.6.1 Potential (potentielle Energie):
Eine Funktion U(x) heißt Potential oder potentielle Energie, wenn ![]() gilt.
gilt.
![]()
12.9.6.2 Kinetische Energie:
Sie wird definiert als ![]() .
.
12.9.6.3 Gesamtenergie:
Die Gesamte Energie eines Massenpunktes im Kraftfeld f am Ort x mit dem Impuls p ist die
Summe von kinetischer und potentieller Energie:
![]()
12.9.6.4 Energiesatz:
Für alle Punkte (x,p) einer Phasenkurve gilt der Energiesatz:
![]()
Die Phasenkurven sind Niveaulinien der Energiefunktion bzw. Teile davon.
12.9.7 Lösungsverfahren der speziellen Differentialgleichung:
Es entfallen einige bei der allgemeinen autonomen Differentialgleichung notwendige Annahmen bzw. Schritte. Es darf nun p0 = 0 sein.
1. Schritt: Das Potential wird aus ![]() berechnet.
berechnet.
Die Phasenkurve folgt dann aus dem Energiesatz.
2. Schritt: Der Impuls läßt sich berechnen mit
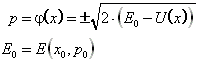
3. Schritt: Man gewinnt die Lösung mit der schon angegebenen Formel ![]() .
.
12.9.8 Autonome Differentialgleichungs-Systeme:
Das allgemeine System lautet: ![]()
Ein singulärer Punkt sei ![]() .
.
12.9.8.1 Linearisiertes System:
Ist v(x) in eine Taylorreihe entwickelbar, so heißt das System
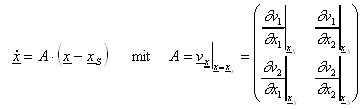
linearisiertes System.
Ermittelt man für das linearisierte System einen singulären Punkt eines bestimmten Typs, so ist er auch ein singulärer Punkt gleichen Typs für das nicht-linearisierte
System.
12.9.9 Klassifizierung von singulären Punkten, Phasenportraits:
| 12.9.9.1 Knotenpunkt: Ein Knotenpunkt liegt vor, wenn die Wurzeln der charakteristischen Gleichung reell sind und gleiches Vorzeichen besitzen. In der Umgebung des singulären Punktes verlaufen alle Phasenkurven durch ihn hindurch und haben hier, falls keine Doppelwurzel vorliegt, eine gemeinsame Tangente. Im Falle einer Doppelwurzel haben die Phasenkurven entweder eine gemeinsame Tangente, oder durch den singulären Punkt verläuft in jeder Richtung eine eindeutige Kurve. Handelt es sich um ein lineares autonomes DGL-System, so werden noch Knotenpunkte 1. Art und Knotenpunkte 2. Art unterschieden. | Knoten 1. Art: 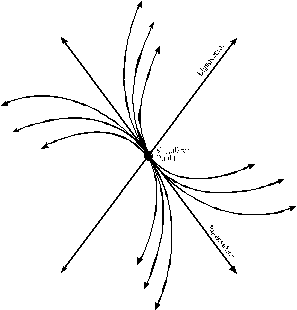 Knoten 2. Art:  |
| 12.9.9.2 Strahlpunkt / Sternpunkt: Als Strahlpunkt bezeichnet man einen Knotenpunkt, durch den Phasenkurven
der Form y = C·x gehen. | 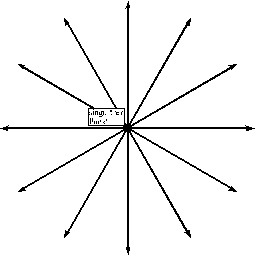 |
| 12.9.9.3 Sattelpunkt: Als Sattelpunkt bezeichnet man einen singulären Punkt, durch den genau zwei
Phasenkurven verlaufen. Die Wurzeln der charakteristischen Gleichung sind
dann reell und besitzen verschiedenes Vorzeichen. Sattelpunkte sind immer
instabil. | 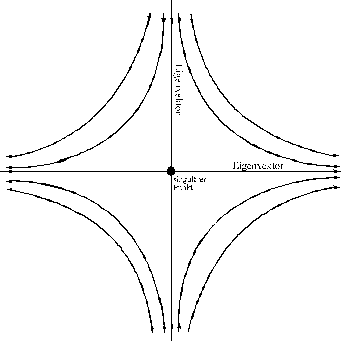 |
| 12.9.9.4 Strudelpunkt: Sind die Wurzeln der charakteristischen Gleichung konjugiert-komplex,
dann ist der singuläre Punkt ein Strudelunkt, auf den sich die Phasenkurven in
unendlich vielen Windungen aufwinden. | 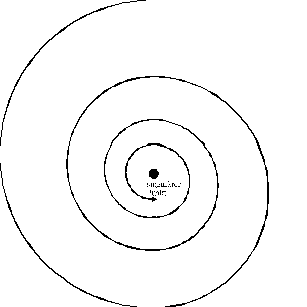 |
| 12.9.9.5 Wirbelpunkt: Ein singulärer Punkt, in dessen Umgebung ausschließlich geschlossene Phasenkurven liegen, heißt Wirbelpunkt. Die charakte-ristische Gleichung muß rein imaginäre Wurzeln haben. Gilt für einen singulären Punkt (x0,0), daß zu jedem e > 0 ein d > 0 existiert, wobei für eine Wahl des Anfangspunktes (x10, x20) mit dem Abstand d 1 < d zum singulären Punkt die zugehörige Phasenkurve einen Abstand d2 < e zum singulären Punkt hat, dann heißt der singuläre Punkt stabil. Die Pfeilrichtung der Phasenkurve weist auf den singulären Punkt. Ist diese Bedingung nicht erfüllt, so heißt der singuläre Punkt instabil. | 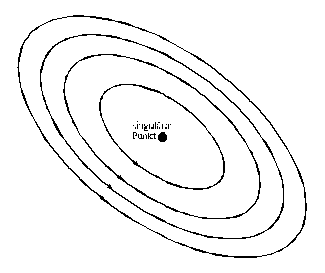 |
12.9.9.6 Stabilitätskarte für lineare autonome DGL-Systeme im ![]() :
:
DGL-System: ![]()
Bezeichnungen:
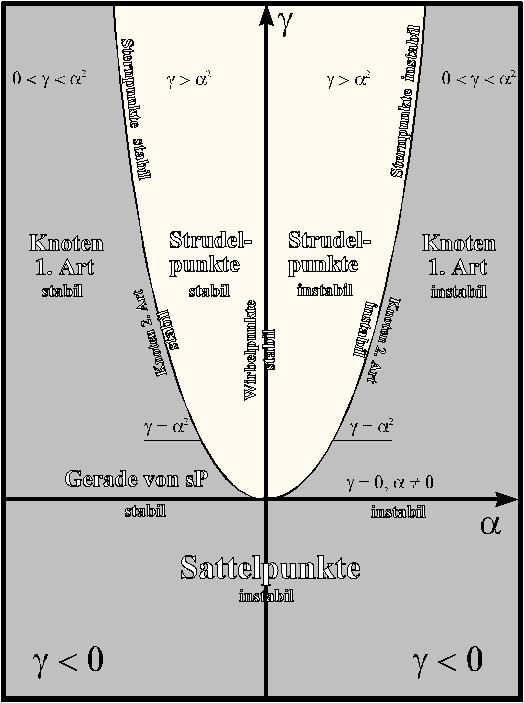
1. Fall: Sattelpunkt: ![]() . Die Eigenwerte haben verschiedenes Vorzeichen.
. Die Eigenwerte haben verschiedenes Vorzeichen.
2. Fall: Gerade von singulären Punkten: ![]() . Ein Eigenwert ist null, der andere nicht.
. Ein Eigenwert ist null, der andere nicht.
3. Fall: Knoten 1. Art: ![]() . Die Eigenwerte haben gleiches Vorzeichen.
. Die Eigenwerte haben gleiches Vorzeichen.
4. Fall: ![]() . Es gibt nur einen Eigenwert.
. Es gibt nur einen Eigenwert.
4.1: Sternpunkt: Die Eigenvektoren spannen den
auf.
4.2: Knoten 2. Art: Die Eigenvektoren spannen den
nicht auf.
5. Fall: Strudelpunkt: ![]() Die Eigenwerte sind konjugiert-komplex.
Die Eigenwerte sind konjugiert-komplex.
Eine Funktion heißt homogen mit dem Homogenitätsgrad m, wenn sie die folgende Bedingung für beliebige l erfüllt:
![]()
Kapitel 13: Fourierreihen