![]()
13. Fourierreihen
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
13.1 Trigonometrische Polynome und minimale Integralmittel
Eine skalare Funktion f(x) heißt periodisch mit der Periode T > 0 oder auch T-periodisch, falls f(x) = f(x + T) für alle reellen x gilt.
Ist eine solche Funktion f T-periodisch, so ist
2p-periodisch. Die folgenden Betrachtungen beziehen sich ausschließlich auf 2p-periodische Funktionen.
13.1.2 Trigonometrisches Polynom n-ten Grades:
So bezeichnet man folgendes Polynom:
13.1.3 Primäre Problemstellung:
Gegeben sei eine 2p-periodische Funktion f.
13.1.3.1 Kann f durch ein bestimmtes trigonometrisches Polynom besonders gut angenähert werden ?
13.1.3.2 Was heißt "gute Annäherung" überhaupt, wo f doch nicht einmal stetig sein muß, aber jedes Tn stetig ist ?
13.1.3.3 Welche zusätzlichen Forderungen sind an f bzw. an die Koeffizienten ak, bk zu stellen so daß die formale Reihe
![]()
konvergiert ?
13.1.3.4 Wenn Sf (x) für ein reelles x existiert, gilt dann f(x) = Sf(x) ?
Als Maß der Annäherung wählt man das sogenannte Integralmittel:
13.1.5 Fourierkoeffizienten (FK):
Minimiert man das Integralmittel, so ergibt sich Folgendes:
Existieren diese Integrale, so heißen die Terme Fourierkoeffizienten (FK) von f.
13.1.6 Unterscheidung bei geraden und ungeraden Funktionen:
Sei eine 2p-periodische Funktion f(x) gegeben, deren Fourierkoeffizienten für alle k existieren. Dann gilt:
f ist eine gerade Funktion:
f ist eine ungerade Funktion:
Ist f stetig im Intervall [-p,p] und 2p-periodisch, dann gilt:
Die Fourierkoeffizienten streben gegen null, wenn k gegen unendlich geht.
Ist f stetig und stückweise glatt im Intervall [-p,p] sowie 2p-periodisch, dann konvergiert die Fourierreihe gleichmäßig und absolut, und es gilt:
Betrachtet man eine allgemeine 2L-periodische Funktion f, so gilt für die Fourierreihe:
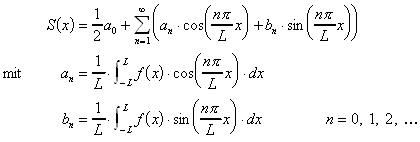
Dieser wird aus dem trigonometrischen Polynom gewonnen.
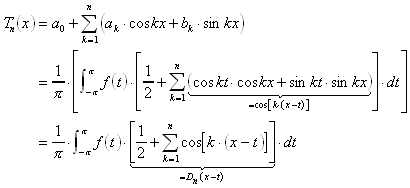
Der Dirichlet-Term hat folgende Eigenschaften:
Daraus folgt für das trigonometrische Polynom:
13.1.10 Fourierreihenentwicklungen einiger 2p-periodischer Funktionen:
| Funktion | Fourierreihe |
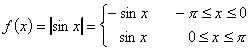 | 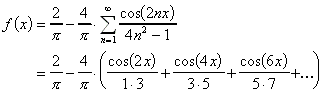 |
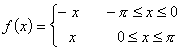 | 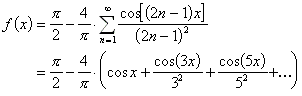 |
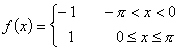 | 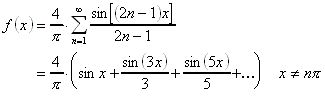 |
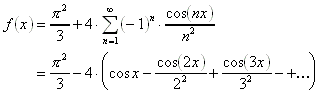 | |
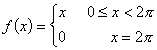 | 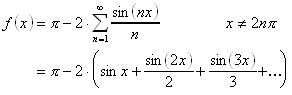 |
13.2 Eine Anwendung auf die Saitenschwingung
Gegeben sei eine Saite der Länge p, die an beiden Enden eingespannt sei und auf die keine äußeren Kräfte einwirke.
13.2.1 Zugehöriges Randwertproblem:
13.2.2 Separierte Differentialgleichungen:
Man erhält als Ansatz:
13.2.3 Ermittlung der Eigenfunktionen:
Unter Berücksichtigung der Anfangs- und Randwerte ergibt sich:
13.2.4 Lösung der Differentialgleichung:
13.2.5 Fourierreihen von f bzw. g:
Falls ![]() existiert und Differentiation und Summation vertauschbar sind, so folgt:
existiert und Differentiation und Summation vertauschbar sind, so folgt:
Dies sind die Fourierreihen von f bzw. g.
Kapitel 14: Kurven und Flächen