14. Kurven und Flächen
             Kein Frame mit dem Inhaltsverzeichnis ?  => Frameset laden

14.1 Kurven im und

14.1.1 Parameterdarstellung eines Kurvenbogens, Parametertransformation:

heißt Parameterdarstellung eines Kurvenbogens, wenn x(t) stetig und differenzierbar ist, sowie die Ableitung nach t im Intervall [a,b] nicht null ist.

Eine Parametertransformation heißt "zulässig", wenn sie bijektiv und stetig ist, sowie überall eine positive Ableitung besitzt. Bei zulässigen Parametertransformationen ändert sich die Richtung einer Tangente nicht.

14.1.2 Spezielle zulässige Parametertransformation auf "Bogenlänge":

Die Länge einer allgemeinen Kurve lautet:

Dies ist eine zulässige Parametertransformation.

14.1.3 Tangentenvektor, Normalenvektor und Krümmung einer Kurve im :

Tangentenvektor: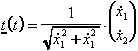

Normalenvektor: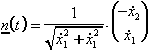

Krümmung: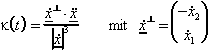

14.1.4 Begleitendes Dreibein einer Kurve im :

Sei x(s) eine Parameterdarstellung einer Kurve im parametrisiert nach der Bogenlänge.

Dann heißen Tangentenvektor,

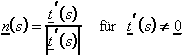Hauptnormalenvektor

und Binormalenvektor.

heißt begleitendes Dreibein der Kurve. Es bildet eine Orthogonalbasis des .

14.1.5 Frenetsche Formeln:

Sei x(s) eine Parameterdarstellung einer Kurve im parametrisiert nach der Bogenlänge. sei das begleitende Dreibein.

Man nennt dann Krümmung und

Torsion oder Windung.

Daraus folgt dieses Differentialgleichungs-System:

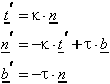
Mit x' = t ist x(s) dann bis auf eine Translation eindeutig bestimmt.

14.1.6 Bezüglich der Zeit parametrisierte Kurven im :

Tangentenvektor:

Binormalenvektor:

Hauptnormalenvektor:

Krümmung: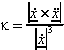

Torsion / Windung: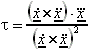

14.2 Einführung in die lokale Theorie der Flächen im

14.2.1 Parameterdarstellung eines Flächenstückes, Parametertransformation:

heißt Parameterdarstellung eines Flächenstücks x(G) im , falls x in G stetig differenzierbar ist und für alle (u,v) aus G gilt:

Eine Parametertransformation

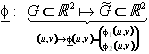
heißt zulässig, falls f bijektiv und stetig differenzierbar ist. Darüber hinaus muß die Jacobideterminante positiv sein. für alle (u,v) aus G.

Ist f eine zulässige Parametertransformation, dann ändert sich die Richtung von unter f nicht.

Normalenvektor der Fläche x(G):

14.2.2 Kurven auf Flächen:

Sei die Parameterdarstellung einer ebenen Kurve in G. Dann ist die Parameterdarstellung einer Kurve auf der Fläche x(G).

Deren Tangentenvektor ist gegeben durch:

Die Tangente liegt in der von x_u und x_v aufgespannten Ebene.

14.2.3 Koeffizienten der 1. Fundamentalform:

Die Bogenlänge wird bestimmt durch

E, F, G heißen Koeffizienten der 1. Fundamentalform.

Schreibweise:

14.2.4 Eigenschaften, Anwendungen:

Sei die Parameterdarstellung der Fläche x(G) und E, F, G die Koeffizienten der 1. Fundamentalform. Dann kann Folgendes formuliert werden:

14.2.4.1 Ist die Parameterdarstellung einer Kurve in G, und die Verkettung von x und g verbinde auf G die Punkte a und b. Dann gilt für die Bogenlänge s der Flächenkurve:

14.2.4.2 Seien g₁ und g₂ die Parameterdarstellungen zweier Kurven in G, die sich für ein t schneiden. Dann schneiden sie sich unter dem Winkel a mit

14.2.4.3 Durch wird der Flächeninhalt des von x_u und x_v aufgespannten Parallelogramms bestimmt.

14.2.5 Flächen in expliziter Form:

Es gilt allgemein:

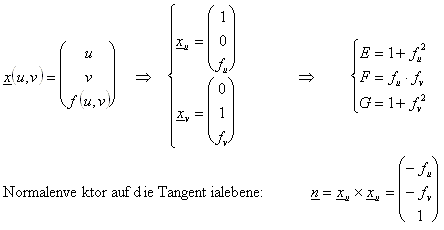
Kapitel 15: Kurven- und Oberflächenintergale