1. Zahlbereiche und ihre Eigenschaften
         Kein Frame mit dem Inhaltsverzeichnis ?  => Frameset laden

1.1 Natürliche Zahlen

Symbol:

1.2 Ganze Zahlen

Symbol:

1.3 Rationale Zahlen

Symbol:

1.4 Reelle Zahlen

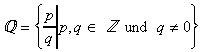
Symbol:

1.4.1 Axiome der Addition:

1.4.1.1 a + b = b + a

1.4.1.2 (a + b) + c = a + (b + c)

1.4.1.3 Die Gleichung a + x = b ist immer eindeutig lösbar.

1.4.1.4 - (-a) = a

1.4.2 Axiome der Multiplikation:

1.4.2.1 a × b = b × a

1.4.2.2 (a × b) × c = a × (b × c)

1.4.2.3 a × (b + c) = a × b + a × c

1.4.2.4 Die Gleichung a × x = b ist für alle a0 eindeutig lösbar.

1.4.3 Axiome der Ordnung:

1.4.3.1 a < b und b < c a < c

1.4.3.2 a < b; c beliebig a + c < b + c

1.4.3.3 a < b; c > 0 a × c < b × c

1.4.4 Archimedisches Axiom:

Zu jeder reellen Zahl x gibt es eine natürliche Zahl n, für die gilt: n > |x|

Zu jeder reellen Zahl x > 0 gibt es eine natürliche Zahl n, für die gilt: n-1 < x

1.4.5 Axiom der Vollständigkeit:

Jede Verknüpfung zweier reeller Zahlen gemäß dieser Axiome ergibt wieder eine reelle Zahl.

1.4.6 Bemerkung:
Dreiecksungleichung:

1.5 Komplexe Zahlen

Symbol:

Die Menge der komplexen Zahlen ist ein algebraischer Körper bezüglich Addition und Multiplikation.

Imaginäre Einheit:

1.5.1 Schreibweisen:

Schreibweise einer komplexen Zahl z:

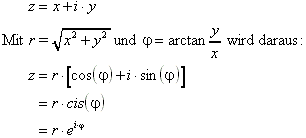
Es gilt die Dreiecksungleichung.

1.5.2 Die Moivre'sche Formel:

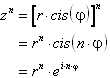
Die Exponentialschreibweise von z wird als Polarform von z bezeichnet.

1.6 Das Prinzip der vollständigen Induktion

Es sei n₀ eine natürliche Zahl und A(n) für alle natürlichen Zahlen eine Aussage. Es gelte:

1.6.1 Induktionsanfang: A(n₀) ist eine wahre Aussage.

1.6.2 Induktionsvoraussetzung: Die Annahme der Gültigkeit dieser Aussage für alle

1.6.3 Induktionsschluß: [A(n) A(n+1)] ist wahr für alle
Damit ist die Gültigkeit der Aussage A(n) bewiesen.

1.6.4 Beispiel: Bernoullische Ungleichung:

Es sei x eine reelle Zahl mit . Ferner sei n eine natürliche Zahl. Dann gilt für alle n die Bernoullische Ungleichung:

Beweis unter Verwendung vollständiger Induktion:

Induktionsanfang: (gilt insbesondere für )

Induktionsannahme: Die Behauptung gelte für ein , also.

Induktionsschluß: Zu zeigen ist, daß die Behauptung dann auch für n + 1 gilt, also

. Außerdem gilt: Da ist, ist .

Daraus folgt:

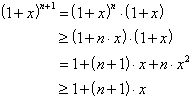
Damit ist die Gültigkeit der Bernoullischen Ungleichung bewiesen.

1.7 Fakultät, Binomialkoeffizient, Binomischer Lehrsatz

1.7.1 Die Fakultät:

1.7.2 Der Binomialkoeffizient:

1.7.3 Der Binomische Lehrsatz:

(siehe Pascalsches Dreieck)

Der binomische Lehrsatz kann mittels vollständiger Induktion bewiesen werden.

1.7.4 Pascal'sches Dreieck:

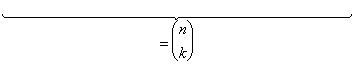
1.8 Der Fundamentalsatz der Algebra

Ein Polynom n-ten Grades kann immer folgendermaßen umgeformt werden:

Die Zahlen zi heißen Nullstellen des Polynoms P.

Jedes Polynom ungeraden Grades mit reellen Koeffizienten hat mindestens eine reelle Nullstelle.

Kapitel 2: Vektorrechnung, analytische Geometrie, lineare Gleichungssysteme