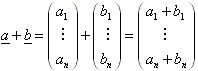
2. Vektorrechnung, analytische Geometrie, lineare Gleichungssysteme
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
2.1 Vektorrechnung, analytische Geometrie
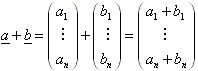
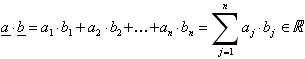
Zusätzlich gilt: ![]()
2.1.4 Schwarzsche Ungleichung:
Ferner gilt die Dreiecksungleichung
2.1.5 Orthogonale Projektion von a auf b:
2.1.6 Winkel zwischen zwei Vektoren a und b:
2.1.7 Raumprodukt (Spatprodukt):
Es erzeugt es ein Rechtssystem, falls es positiv ist, und ein Linkssystem, falls es negativ ist.
Das Vektortripel heißt ausgeartet (linear abhängig), falls das Spatprodukt null ist.
2.1.8 Vektorprodukt (Kreuzprodukt):
Ist das Kreuzprodukt null, so sind die beiden Vektoren linear abhängig.
2.1.9 Vektorielle Darstellung einer Gerade in Punkt-Richtungsform:
2.1.10 Vektorielle Darstellung einer Gerade in Hesseform:
2.1.11 Vektorielle Darstellung einer Gerade in Hesse-Normalenform:
Die Darstellungsarten in Hesseform sind nur im zweidimensionalen Vektorraum möglich, im dreidimensionalen Raum repräsentieren sie Ebenen.
2.1.12 Plückerform einer Gerade im dreidimensionalen Vektorraum:
2.1.13 Darstellung einer Ebene in Punkt-Richtungsform:
2.1.14 Darstellung einer Ebene in Hesseform:
2.1.15 Darstellung einer Ebene in Hesse-Normalenform:
2.1.16 Umrechnungsformeln der Ebenenformen:
2.1.17 Graßmannscher Entwicklungssatz:
Dieser Satz gilt nur für Vektoren aus V3.
2.1.18 Identität von Lagrange:
Eine Linearkombination aus n Vektoren des Grades n bildet ein lineares Gleichungssystem, wenn ein bestimmter Vektor als Ergebnis der Linearkombination
gefordert wird. Ist dieser Vektor der Nullvektor, so spricht man von einem homogenen Gleichungssystem, andernfalls von einem inhomogenen
Gleichungssystem.
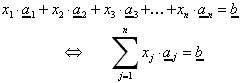
Ein LGS ist lösbar, falls genügend linear unabhängige Gleichungen vorhanden sind. Sind bei einem LGS vom Rang n (d.h. mit n Unbekannten) nur r linear
unabhängige Gleichungen gegeben, so beträgt der Defekt d des Gleichungssystems: d = n - r.
2.2.1 Allgemeines Lösungsverfahren:
Zunächst wird die Hauptdeterminante D berechnet, was bis Rang n = 3 ohne weitere Umformungen möglich ist. Ist der Rang n > 3, ist meistens der Gauß'sche
Algorithmus am günstigsten.
1. Fall: D = 0: keine eindeutige Lösung ![]() Gauß'scher Algorithmus (Lösungsmenge ist eine Ebene oder eine Gerade)
Gauß'scher Algorithmus (Lösungsmenge ist eine Ebene oder eine Gerade)
2. Fall: D![]() 0: eindeutige Lösung
0: eindeutige Lösung ![]() Cramer'sche Regel (Determinantenverfahren)
Cramer'sche Regel (Determinantenverfahren)
Zum Schluß wird die Lösungsmenge als Vektor oder Zahlentupel aufgeschrieben.
2.2.2 Der Gauß'sche Algorithmus:
Das Prinzip besteht darin, eine Gleichung dazu zu benutzen, aus den restlichen eine Unbekannte zu eliminieren. Dies wird dann so lange fortgesetzt, bis nur noch eine Gleichung mit einer Unbekannten vorhanden ist. Danach wird rückwärts in alle Gleichungen eingesetzt, womit man alle Unbekannten erhält und das LGS löst.
Die folgenden zwei Beispiele zeigen ein eindeutig lösbares und ein nicht eindeutig lösbares LGS.
1. Beispiel:
Folgendes LGS ist gegeben. Gesucht ist dessen Lösungsmenge.
| x1 | x2 | x3 | x4 | Operation | ||
| I | 1 | 2 | 3 | 4 | -2 | |
| II | 2 | 3 | 4 | 1 | 2 | |
| III | 3 | 4 | 1 | 2 | 2 | |
| IV | 4 | 1 | 2 | 3 | -2 | |
| V | 1 | 2 | 3 | 4 | -2 | |
| VI | 0 | -1 | -2 | -7 | 6 | =II-2I |
| VII | 0 | -2 | -8 | -10 | 8 | =III-3I |
| VIII | 0 | -7 | -10 | -13 | 6 | =IV-4I |
| IX | 1 | 2 | 3 | 4 | -2 | |
| X | 0 | -1 | -2 | -7 | 6 | |
| XI | 0 | 0 | -4 | 4 | -4 | =VII-2VI |
| XII | 0 | 0 | 4 | 36 | -36 | =VIII-7VI |
| XIII | 1 | 2 | 3 | 4 | -2 | |
| XIV | 0 | -1 | -2 | -7 | 6 | |
| XV | 0 | 0 | -4 | 4 | -4 | |
| XVI | 0 | 0 | 0 | 40 | -40 | =XI+XII |
Durch rückwärtiges Lösen der Gleichungen XVI bis XIII erhält man:
x1 = 0
x2 = 1
x3 = 0
x4 = -1
Die Probe durch Einsetzen bestätigt dieses Ergebnis.
2. Beispiel:
Folgendes LGS ist gegeben. Es enthält mehr Gleichungen als Unbekannte.
| x1 | x2 | x3 | Operation | ||
| I | -1 | -3 | -12 | -5 | |
| II | -1 | 2 | 5 | 2 | |
| III | 0 | 5 | 17 | 7 | |
| IV | 3 | -1 | 2 | 1 | |
| V | 7 | -4 | -1 | 0 | |
| VI | -1 | -3 | -12 | -5 | |
| VII | 0 | -5 | -17 | -7 | =I-II |
| VIII | 0 | 5 | 17 | 7 | =III |
| IX | 0 | -10 | -34 | -14 | =3I+IV |
| X | 0 | -25 | -85 | -35 | =7I+V |
| XI | -1 | -3 | -12 | -5 | |
| XII | 0 | -5 | -17 | -7 | |
| XIII | 0 | 0 | 0 | 0 | |
| XIV | 0 | 0 | 0 | 0 | |
| XV | 0 | 0 | 0 | 0 |
Eine Lösung existiert, sie ist aber nicht eindeutig. Es kann eine Unbekannte als Parameter wählen, z.B. x3.
Die Lösung lautet dann:
Die geometrische Deutung der Lösungsmenge eines LGS mit drei Unbekannten ist die Bestimmung der Schnittmenge der durch die drei Gleichungen des LGS
gegebenen Ebenen. In diesem Beispiel ist die Lösungsmenge eine Gerade:
Ist die Determinante D der Koeffizientenmatrix eines LGS nicht null, dann lassen sich die Unbekannten xk sofort berechnen. Man berechnet dabei zur Bestimmung
z.B. der Unbekannten x3 die Determinante D3, die sich durch Vertauschen des 3.Spaltenvektors der Koeffizientendeterminante mit dem Vektor der absoluten
Glieder ergibt. Aus diesen beiden Determinanten berechnet sich die Unbekannte x3 als deren Quotient.
Allgemein:
![]()
Die mit der Cramer'schen Regel berechneten Lösungen sind immer eindeutig.
Kapitel 3: Matrizen, Matrixalgebra