8. Anwendung der Differentialrechnung
Kein Frame mit dem Inhaltsverzeichnis ? => Frameset
laden
8.1 Der Mittelwertsatz und einfache Anwendungen
Ist eine stetige Funktion f(x) an den Rändern eines Intervalls [a,b] null ( d.h. f(a)=0 und f(b)=0 )
und innerhalb dieses Intervalls differenzierbar, so hat diese Funktion innerhalb
dieses Intervalls mindestens ein
Extremum mit f'(x)=0.
8.1.2 Erster Mittelwertsatz der Differentialrechnung:
Im Intervall [a,b] sei f(x) stetig und differenzierbar. Dann gibt es in [a,b] mindestens ein x, für das gilt:
8.1.3 Addition einer Konstanten:
Sind die Funktionen f und g differenzierbar im Intervall [a,b] und gilt f'(x) = g'(x) für alle x dieses Intervalls, so gibt es eine Konstante C, für die gilt: f = g + C.
8.1.4 Regel von l'Hospital für den Fall 
:
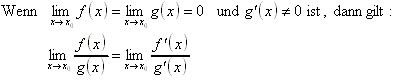
8.1.5 Regel von l'Hospital für den Fall 
:
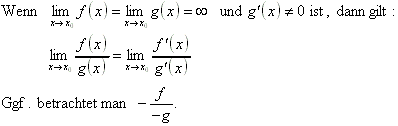
8.1.6 Grenzwerte anderer Formen:
Grenzwerte der Formen 
können auf die Fälle 
oder 
zurückgeführt werden.
8.2 Taylorformel und Taylorreihe bei Funktionen einer Veränderlichen
Jede Funktion f(x) läßt durch ein Polynom Tn(x) darstellen, für das gilt:
.
Hierbei ist Rn(x) ein Restglied ist, das den vorhandenen Fehler ausgleicht.
Ist die Funktion f(x) (n+1)-fach differenzierbar, so gilt für deren Taylorpolynom:
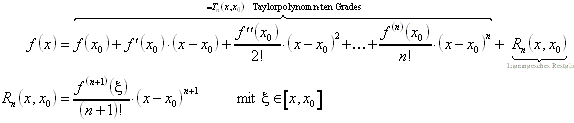
Beispiel: Taylorformel um x0 = 0 für die Funktion f(x) = ex innerhalb des Intervalls [-1,1].
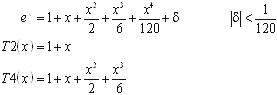
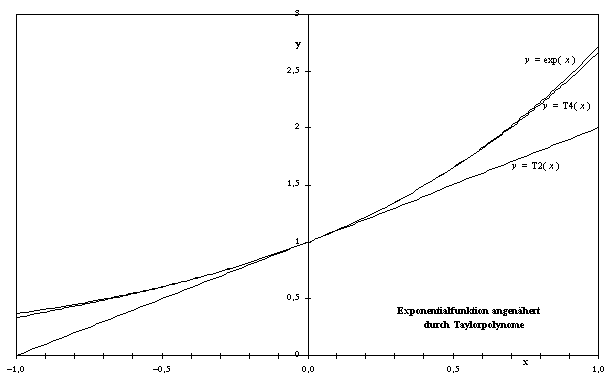
8.2.2 Taylorreihe, MacLaurin-Reihe:
Ist die Funktion f(x) beliebig oft differenzierbar, so konvergiert deren Taylorreihe, welche folgendermaßen lautet:
Für x0 = 0 heißt sie MacLaurin-Reihe.
Beispiel: Die MacLaurin-Reihenentwicklung der folgenden Funktion f(x):
Vorgehensweise:
Erstens: Bestimmung des Definitionsbereiches
Zweitens: Bestimmung der Nullstellen (mit der x-Achse)
Drittens: Bestimmung der Unstetigkeitsstellen bzw. der Grenzwerte der Funktion (falls möglich) an den Rändern des Definitionsbereiches
Viertens: Bestimmung der Ableitung an den Rändern des Definitionsbereiches
Fünftens: Bestimmung des qualitativen Verlaufs des Graphen mit relativen Extremwerten (Nullstellenmenge von f'(x) )
Sechstens: Bestimmung der Wendepunkte ( Nullstellenmenge von f''(x) )
Siebtens: Bestimmung von Monotonieintervallen ( einheitlich in den Bereichen zwischen den Nullstellen von f'(x) )
Achtens: Bestimmung von Konvexitäts- und Konkavitätsbereichen
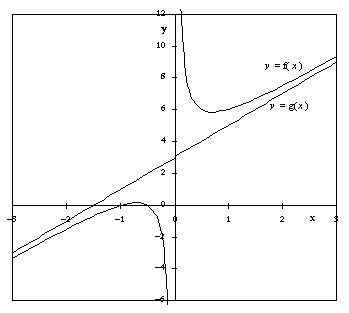
Eine Asymptote an eine Funktion f(x) ist diejenige Gerade g(x) = ax + b, für die gilt:
Bestimmung von g(x):
Die Funktion f(x) hat eine senkrechte Asymptote an der Stelle x0, falls sie dort einen uneigentlichen Grenzwert besitzt.
Beispiel: (Graph s. rechts) Asymptoten an die Funktion f(x):
|  |
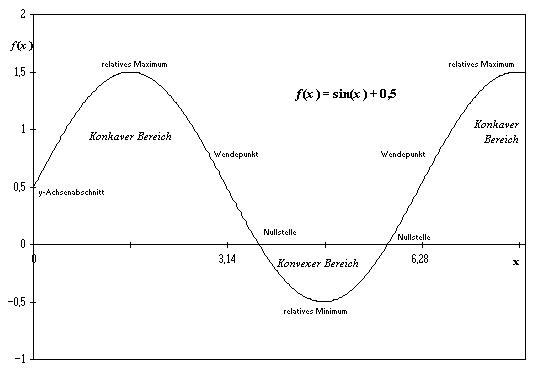
8.3.2.1 Konvexitätskriterium: Ist die erste Ableitung f'(x) einer Funktion f(x) in einem Intervall [a,b] monoton steigend, d.h. die zweite Ableitung
f''(x) > 0, so heißt die Funktion f(x) konvex auf [a,b].
8.3.2.2 Konkavität: Eine Funktion f(x) heißt konkav auf [a,b], wenn -f(x) dort konvex ist.
Beispiel: Graph der Funktion f(x) = sin(x) + 0,5
8.4 Satz von Taylor für Funktionen mehrerer Veränderlicher, Anwendungen auf Extremwertaufgaben
8.4.1 Taylorsche Reihe für Funktionen zweier Veränderlicher:
8.4.1.1 Erste Form der Darstellung:
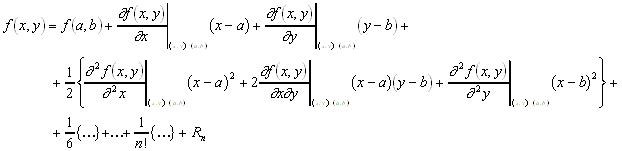
8.4.1.2 Zweite Form der Darstellung:
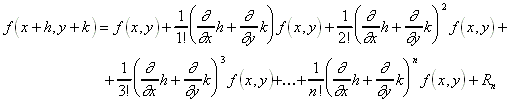
8.4.1.3 Das Restglied lautet:
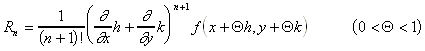
8.4.2 Taylorsche Reihe für Funktionen von m Veränderlichen:
Die Darstellung erfolgt analog mit Differentialoperatoren.
8.4.2.1 Taylor-Reihe:
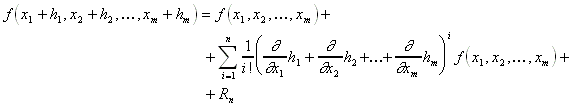
8.4.2.2 Restglied:
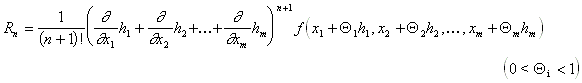
8.4.3 Relative und absolute Extrema:
8.4.3.1 Eine Funktion f besitzt im Punkt x0 ein strenges relatives Maximum, wenn die Funktionswerte der Punkte des nächsten Umkreises (d > 0) um f(x0) vom Betrag kleiner sind als f(x0). Bei relativen Maxima ist die Gleichheit der Funktionswerte zugelassen. f(x0) ist ein entsprechendes Minimum, wenn - f(x0) ein entsprechendes Maximum ist.
8.4.3.2 Eine Funktion f besitzt im Punkt x0 ein strenges absolutes Maximum, wenn die Funktionswerte aller anderen Punkte im Definitionsbereich von f vom Betrag kleiner sind als f(x0). Bei absoluten Maxima ist die Gleichheit der Funktionswerte zugelassen. f(x0) ist ein entsprechendes Minimum, wenn -f(x0) ein entsprechendes Maximum ist.
8.4.3.3 Ein Sattelpunkt liegt vor, wenn eine Funktion f an der Stelle x0 zwar nur Ableitungen vom Betrag Null hat, die obenstehenden Bedingungen aber nicht erfüllt sind.
Beispiel: Der Punkt (0,0) der folgenden Funktion ist ein Sattelpunkt.
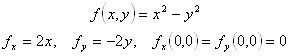
8.4.4 Hinreichende Bedingung für strenge relative Extrema:
Eine Funktion f sei im Intervall 
2-fach differenzierbar und bilde 
auf 
ab. Es sei der Vektor 
.
8.4.4.1 Strenge relative Maxima:
Wenn nun 
und 
während 
ist, dann liegt in (x0,y0) ein strenges relatives
Maximum vor.
8.4.4.2 Strenge relative Minima:
Wenn nun 
und 
während 
ist, dann liegt in (x0,y0) ein strenges relatives
Minimum vor.
8.4.5 Satz über implizite Funktionen:
Es sei n,m mit n>m und 
offen, 
, es gelte ferner:
1.) 
ist k-fach stetig partiell differenzierbar,
2.) 
und
3.) 
ist nichtsingulär, der Betrag der Determinante der Ableitungmatrix also ungleich Null.
Dann gibt es eine offene Umgebung 
von x0 und eine offene Umgebung 
von y0 mit 
und es existiert eine k-fach partiell
differenzierbare implizite Funktion 
. Sie hat folgende Eigenschaften:
a) 
Insbesondere: 
.
b) 
Insbesondere: 
.
Angewendet werden kann dieser Satz beispielsweise auf nichtlineare Gleichungssysteme, deren Variablen in Abhängigkeit einer anderen dargestellt werden sollen.
Beispiel:
Gegeben ist das folgende nichtlinare Gleichungssystem:
Geschrieben im Format nach dem Satz über impliziten Funktionen:
Gesucht sind nun y(x) und z(x).
Die Voraussetzungen 1.) bis 3.) sind erfüllt. Es ist
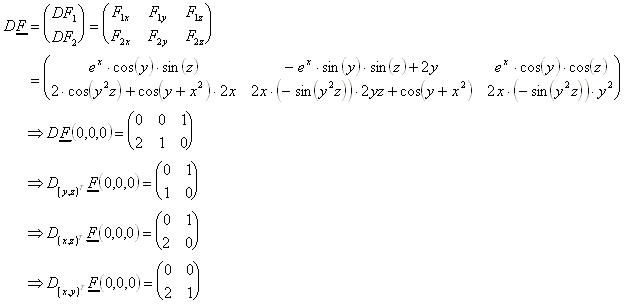
Aus den Beträgen der jeweiligen Determinanten wird sofort ersichtlich, daß nach y(x) und z(x) sowie nach x(y) und z(y) aufgelöst werden kann. Dagegen ist für die
Auflösung nach x(z) und y(z) die Anwendung des Satzes über Implizite Funktionen für die nicht möglich.
8.4.6 Die Lagrangesche Multiplikatorregel:
8.4.6.1 Es seien die Funktionen 
stetig partiell differenzierbar. Ferner liege an der Stelle x0 ein relatives Extremum von f eingeschränkt auf die
Menge 
vor. Außerdem gelte 
. Dann gibt es ein 
mit 
.
8.4.6.2 Lagrangesche Funktion L: 
8.4.6.3 Lagrangescher Multiplikator l :
Beispiel:
Gesucht werden die Scheitelpunkte der Ellipse gegeben durch 
.
Formuliert man die Aufgabenstellung gemäß der Lagrangeschen Multiplikatorregel um, so ergibt sich 
(Kreisgleichung) unter der Bedingung, daß
.
Die entsprechende Lagrangesche Funktion lautet dann:
Daraus folgt dann
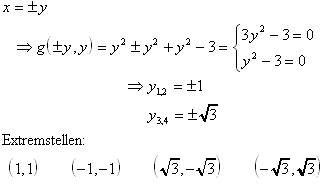
8.5 Fehler- und Ausgleichungsrechnung
Physikalisch ermittelte (gemessene) Zusammenhänge und deren entsprechend beschreibende Funktion stimmen nie genau überein. Es bleibt immer eine Differenz zwischen der Folge der gemessenen Werte und der eigentlichen Funktion. Man kann diese Funktion den gemessenen Werten anpassen, indem sie so zwischen die Folge der Meßwerte gelegt wird, daß die Summe der Quadrate der jeweiligen Differenz minimal wird.
Geht man aus von der Funktion
,
bei der ai Parameter sind, die bei einer Vorgabe von k Meßpunkten 
so bestimmt werden sollen, daß die quadratische
Fehler-Funktion 
definiert durch
in 
ein Minimum hat. Im linearen Fall bestimmt man anhand der Meßpunkte die Ausgleichsgerade f(x,a,b) = ax + b.
8.5.1 Das Fehlerfortpflanzungsgesetz:
8.5.1.1 Systematische Fehler entstehen durch meßtechnische Mängel und können nur durch
Verbesserung der jeweiligen Meßapparatur minimiert werden.
8.5.1.2 Statistische Fehler sind auf Meßungenauigkeit beeinträchtigende Vorkommnisse
zurückzuführen, wie beispielsweise Ablesefehler, Luftfeuchtigkeit,... Verbessert werden
sie durch häufige Wiederholung derselben Messung.
8.5.2 Arithmetischer Mittelwert, Streuung:
Für sie gilt:
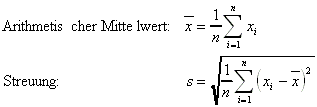
Kapitel 9: Integralrechnung
